Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a;Vì AB//CD nên theo định lí Ta-lét ta có:
\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
\(\Rightarrow OA.OD=OC.OB\)
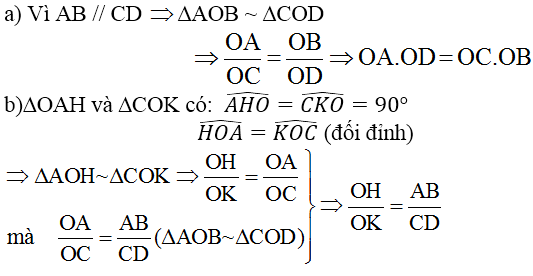
b;Xét \(\Delta AOH\) và \(\Delta COK\)có:
\(\widehat{AHO}=\widehat{CKO=90^o}\)
\(\widehat{AOH}=\widehat{COK}\) (hai góc đối đỉnh)
\(\Rightarrow\Delta AOH~\Delta COK\left(g.g\right)\)
\(\Rightarrow\dfrac{OA}{OC}=\dfrac{OH}{OK}\left(1\right)\)
Vì AB//CD nên theo hệ quả của định lí Ta-lét ta có
\(\dfrac{AB}{CD}=\dfrac{OA}{OC}\left(2\right)\)
Từ 1 và 2 ta có:
\(\dfrac{OH}{OK}=\dfrac{AB}{CD}\)

a) AB//CD => góc BAC = góc DCA ( so le trong)
Xét tam giác ABO và tam giác CDO có:
góc BAC = góc DCA (cmt)
góc AOB = góc COD (đối đỉnh)
=> tam giác ABO ~ tam giác CDO (TH3)
=> \(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\)
=> OA. OD = Oc. OB (đpcm)
b) Xét tam giác HOA và tam giác KOC có:
góc HOA = góc KOC (đối đỉnh)
góc BAC = góc DCA (cmt)
=> tam giác HOA ~ tam giác KOC (TH3)
c) Ta có:
+) AB//CD => \(\dfrac{AB}{CD}\) = \(\dfrac{OA}{OC}\)(hệ quả định lí Talet)(1)
+) AB//CD ; H \(\in\) AB; K \(\in\) DC => AH//KC
=> \(\dfrac{OH}{OK}\) = \(\dfrac{OA}{OC}\)( hệ quả định lí Talet)(2)
Từ (1) và (2) => \(\dfrac{AB}{CD}\) =\(\dfrac{OH}{OK}\) (đpcm)
![]()

a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)
\(\widehat{AOB}=\widehat{COD}\)
Do đó; ΔOAB\(\sim\)ΔOCD
Suy ra: OA/OC=OB/OD
hay \(OA\cdot OD=OB\cdot OC\)
b: Ta có; ΔOAB\(\sim\)ΔOCD
nên AB/CD=OB/OD=OA/OC
=>5/CD=OB/3,6=2/4=1/2
=>CD=10cm; OB=1,8(cm)

đề bài: cho hình thanh ABCD (AB//CD). Gọi I là giao điểm của 2 đg chéo AC và BD. Vẽ qua I đường thẳng song song với AB và BC, cắt AD, BC lần lượt tại E,F. chứng minh:
....
bn tự kẻ hình nha :)
a) Xét tg ACD, có: EI // DC
\(\Rightarrow\frac{EI}{DC}=\frac{AI}{AC}\)(1)
Xét tg BCD, có: FI // DC
\(\Rightarrow\frac{FI}{DC}=\frac{IB}{BD}\)(2)
Xét tg ABI, có: AB // CD
\(\Rightarrow\frac{AI}{AC}=\frac{IB}{BD}\) (3)
Từ (1);(2);(3) \(\Rightarrow\frac{IE}{DC}=\frac{IF}{DC}\Rightarrow IE=IF\)
b) Xét tg ACD, EI // DC
=> EI/DC = AE/ AD (1)
Xét tg ADB, EI // AB
=> EI/AB = DE/AD (2)
Từ (1);(2) => \(\frac{EI}{DC}+\frac{EI}{AB}=\frac{AE}{AD}+\frac{DE}{AD}=1\)
\(\Rightarrow EI.\left(\frac{1}{DC}+\frac{1}{AB}\right)=1\Rightarrow\frac{1}{EI}=\frac{1}{DC}+\frac{1}{AB}\)
cmtt, t/có: \(\frac{1}{FI}=\frac{1}{DC}+\frac{1}{AB}\)
\(\Rightarrow\frac{1}{EI}=\frac{1}{FI}=\frac{1+1}{EI+FI}=\frac{2}{EF}=\frac{1}{AB}+\frac{1}{CD}\)

A B C D N M E
a, kẻ AM cắt CD tại E
xét tam giác AMB và tam giác EMD có : góc AMB = góc EMD (đối đỉnh)
DM = MB do M là trung điểm của BD (gt)
góc ABM = góc MDE (so le trong AB // DC)
=> tam giác AMB = tam giác EMD (g-c-g) (1)
=> AM = ME (đn) có M nằm giữa A và E
=> M là trung điểm của AE
N là trugn điểm của AC (gt) ; xét tam giác AEC
=> MN là đường trung bình của tam giác AEC (đn) (2)
=> MN // EC (Đl)
CE // AB
=> MN // AB
b, (2) => MN = EC/2
EC = CD - DE
=> MN = (CD - DE) : 2
(1) => DE = AB
=> MN = (CD - AB) : 2