Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn chiều dương là chiều chuyển động của vật
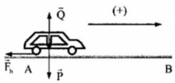
Các lực tác dụng lên vật: trọng lực P → , phản lực N → , lực hãm F h →
Phương trình định luật II Niutơn cho vật:
P → + N → + F h → = m a → (1)
Chiếu (1) lên chiều dương, ta được:−Fh=ma(2)
Mặt khác, ta có phương trình vận tốc:v=v0+at
khi xe dừng lạiv=0→v0=−at(3)
Khi đó, quãng đường đi được của xe
s = v 0 t + 1 2 a t 2 = − a t 2 + 1 2 a t 2 = − 1 2 a t 2 (4)
Từ (4), ta suy ra:
a = − 2 s t 2 = − 2.9 3 2 = − 2 m / s 2
=> thay vào (2), ta có: Lực hãmFh=−ma=−2000.(−2)=4000N
Đáp án: A

Đổi 2 tấn = 2000 kg
36 km/h = 10 m/s
a. Gia tốc của xe là:
\(a=\dfrac{\Delta v}{t}=\dfrac{0-10}{2}=-5\) (m/s)
Độ lớn của lực hãm là:
\(\left|F\right|=\left|ma\right|=10000\) (N)
Hệ số ma sát giữa xe với mặt đường là:
\(\mu=\dfrac{F}{N}=\dfrac{10000}{20000}=0,5\)
b. Quãng đường xe đi được cho đến khi dừng lại là:
\(s=\dfrac{v^2}{2a}=\dfrac{10^2}{2.5}=10\) (m)

Đổi 3 tấn =3000 kg
Độ lớn của v0 là
\(s=v_0t+\dfrac{1}{2}at^2\Rightarrow15=3v_0+\dfrac{9}{2}a\) (1)
\(v^2-v_0^2=2as\Rightarrow-v_0^2=30a\) (2)
Từ (1) và (2) \(\Rightarrow v_0=\dfrac{100}{19}\left(\dfrac{m}{s}\right);a=-\dfrac{10}{57}\left(\dfrac{m}{s^2}\right)\)
Độ lớn lực hãm phanh
\(a=\dfrac{F}{m}\Rightarrow F=a\cdot m=\dfrac{10}{57}\cdot3000\approx526,31\left(N\right)\)

m= 1,2 tấn = 1200kgv= 36km/h = 10m/st=2s
Gia tốc của xe là :a=\(\dfrac{v-v_0}{t}=\dfrac{0-10}{2}=\) -5 m/s
1) quãng đường ô tô đi được kể từ lúc giảm phanh là:
\(s=v_0t+\dfrac{1}{2}at^2\)
\(=10\cdot2+\dfrac{1}{2}\left(-5\right)\cdot2^2\) \(=10m\)
2) vì lực hãm phanh và lực ma sát giữa xe với mặt đường có giá trị bằng nhau nên
Fms = Fh
Fms = ma = 1200 * (-5) = -6000 N⇒ điều này chứng tỏ Fms ngược chừng chiều động của ô tô

Ta có: v=54km/h=15m/s
Chọn chiều (+) là chiều chuyển động, gốc thời gian lúc bắt đầu hãm phanh.
Theo định luật II - Niutơn, ta có:
a → = F → m → a = − F m = − 3000 1000 = − 3 m / s 2
Mặt khác, ta có: v 2 − v 0 2 = 2 as
↔ 0 − 15 2 = 2. ( − 3 ) s → s = 37 , 5 m
Đáp án: A
2.
theo định luật II niu tơn
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\)
chiếu lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động
F-Fms=0 (a=0, xe chuyển động đều )
\(\Rightarrow F=\mu.N\Rightarrow\mu=\dfrac{F}{m.g}\)=0,075
Câu 2:
Tóm tắt:
m=80 tấn=80000kg
Fk=6\(\times\) 104(N)
g=10 m/s2
a=0
\(--------\)
\(\mu=?\)
GIẢI
Áp dụng định luật II Niu-tơn:
\(\overrightarrow{F_{ms}}+\overrightarrow{F_k}+\overrightarrow{P}+\overrightarrow{N}=m\times\overrightarrow{a}\)
Chọn Oxy như hình vẽ:
Trên Ox: \(-F_{ms}+F_k=m\times a\)
\(\Leftrightarrow-\left(\mu\times N\right)+F_k=m\times a\) (1)
Trên Oy: N-P=0
\(\Leftrightarrow N=P=m\times g\) (2)
Từ (1) và (2) \(\Rightarrow-\left(\mu\times m\times g\right)+F_k=m\times a\)
\(\Leftrightarrow-\left(\mu\times80000\times10\right)+6\times10^4=80000\times0\)
\(\Leftrightarrow\mu=0,075\)