Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

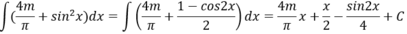
Vì F(0) = 1 nên C =1
F π 4 = π 8 nên tính được m = -3/4
Chọn A.

Biến đổi :
\(\frac{8\cos x}{3\sin^2x+2\sqrt{3}\sin x\cos x+\cos x^2}=\frac{8\cos x}{\left(\sqrt{3}\sin x+\cos x\right)^2}\)
Giả sử :
\(8\cos x=a\left(\sqrt{3}\sin x+\cos x\right)+b\left(\sqrt{3}\cos x-\sin x\right)=\left(a\sqrt{3}-b\right)\sin x+\left(a+b\sqrt{3}\right)\cos x\)
Đồng nhất hệ số hai tử số, ta có hệ :
\(\begin{cases}a\sqrt{3}-b=0\\a+b\sqrt{3}=8\end{cases}\)\(\Leftrightarrow\begin{cases}a=2\\b=2\sqrt{3}\end{cases}\)
Khi đó \(f\left(x\right)=\frac{2}{\sqrt{3}\sin x-\cos x}-\frac{2\sqrt{3}\left(\left(\sqrt{3}\cos x-\sin x\right)\right)}{\sqrt{3}\sin x-\cos x}\)
Trong đó :
\(F\left(x\right)=\int\frac{2dx}{\sqrt{3}\sin x+\cos x}-\frac{2\sqrt{3}\left(\sqrt{3}\cos x-\sin x\right)dx}{\sqrt{3}\sin x+\cos x}=\frac{1}{2}\ln\left|\tan\left(\frac{x}{2}+\frac{\pi}{12}\right)\right|-\frac{2\sqrt{3}}{\sqrt{3}\sin x+\cos x}+C\)
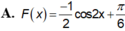
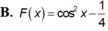
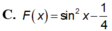
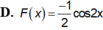
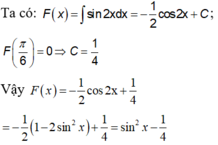
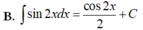
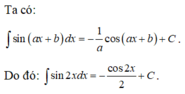
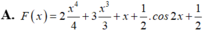
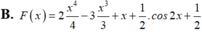
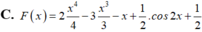
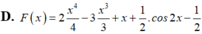
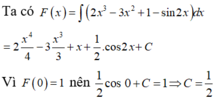
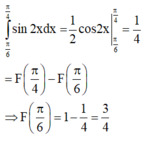




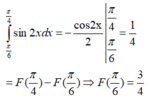
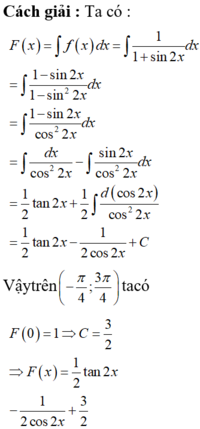
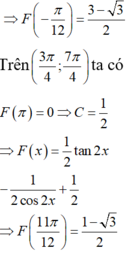
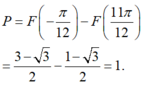
Rất đơn giản là sử dụng nguyêm hàm từng phần:
\(I=\int\left(4x+1\right)sin2x.dx\)
Đặt \(\left\{{}\begin{matrix}u=4x+1\\dv=sin2xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=4dx\\v=-\dfrac{1}{2}cos2x\end{matrix}\right.\)
\(\Rightarrow I=-\dfrac{1}{2}cos2x\left(4x+1\right)+\int2cos2x.dx=-\dfrac{1}{2}cos2x\left(4x+1\right)+sin2x+C\)
Em cảm ơn ạ