Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

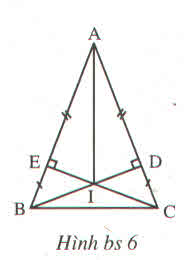
Xét tam giác AIE và tam giác AID có:
AE = AD (theo đề bài)
góc AEI = góc ADI = \(90^0\)
AI là cạng chung
Do đó tam giác AIE = tam giác AID (cạnh huyền và cạnh góc vuông) úuy ra góc A1 = A2 (2 góc tương ứng) (1)
Suy ra: EI = DI (2 cạnh tương ứng)(*)
Xét tam giác IEB và tam giác IDC có:
EI = DI (*)
góc IEB = góc IDC = \(90^0\)
EB = DC ( theo đề bài)
Do đó tam giác IEB = tam giác IDC (2 cạnh góc vuông)
Có BE + AE = AB
CD + AD = AC
mà: AE = AD, EB = DC (theo đề bài)
Suy ra: AB = AC (2)
Xét tam giác AIB và tam giác AIC có:
AB = AC (2)
góc A1 = góc A2 (1)
AI là cạnh chung
Do đó: tam giác AIB = tam giác AIC (c.g.c)
Xét tam giác ECB và tam giác DBC có:
EB = DC ( theo đề bài)
góc CEB = góc BDC = \(90^0\)
Do đó: tam giác ECB = tam giác DBC (cạnh huyền và cạnh góc vuông)
Suy ra: EC = BD (2 cạnh tương ứng) (3)
Xét tam giác AEC và tam giác ADB có:
AE = AD (theo đề bài)
góc AEC = góc ADB = \(90^0\)
EC = BD (3)
Do đó: tam giác AEC = tam giác ADB ( 2 cạnh góc vuông)
Vậy đáp án đúng là: (D) 5 cặp tam giác bằng nhau trong hình bs 6


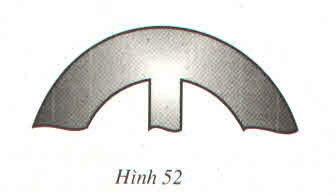
Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A
Hướng dẫn:
Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A

Ghép a-d' ; b –a', c-b', d-c'
Trong một tam giác
a - d' đường phân giác xuất phát từ đỉnh A - là đoạn thẳng có hai mút là đỉnh A và giao điểm của cạnh BC với tia phân giác của góc A.
b - a' đường trung trực ứng với cạnh BC - là đường vuông góc với cạnh BC tại trung điểm của nó.
c - b' đường cao xuất phát từ đỉnh A - là đoạn vuông góc kẻ từ A đến đường thẳng BC.
d - c' đường trung tuyến xuất phát từ đỉnh A - là đoạn thẳng nối A với trung điểm của cạnh BC.
Trả lời
Ghép a-d' ; b –a', c-b', d-c'
Trong một tam giác
a - d' đường phân giác xuất phát từ đỉnh A - là đoạn thẳng có hai mút là đỉnh A và giao điểm của cạnh BC với tia phân giác của góc A.
b - a' đường trung trực ứng với cạnh BC - là đường vuông góc với cạnh BC tại trung điểm của nó.
c - b' đường cao xuất phát từ đỉnh A - là đoạn vuông góc kẻ từ A đến đường thẳng BC.
d - c' đường trung tuyến xuất phát từ đỉnh A - là đoạn thẳng nối A với trung điểm của cạnh BC.

Ghép a-b', b-a', c-d', d-c'
Trong một tam giác
a - b' trọng tâm - là điểm chung của ba đường trung tuyến
b - a' trực tâm - là điểm chung của ba đường cao
c - d' điểm (nằm trong tam giác) cách đều ba cạnh - là điểm chung của ba đường phân giác
d - c' điểm cách đều ba đỉnh - là điểm chung của ba đường trung trực
Trả lời
Ghép a-b', b-a', c-d', d-c'
Trong một tam giác
a - b' trọng tâm - là điểm chung của ba đường trung tuyến
b - a' trực tâm - là điểm chung của ba đường cao
c - d' điểm (nằm trong tam giác) cách đều ba cạnh - là điểm chung của ba đường phân giác
d - c' điểm cách đều ba đỉnh - là điểm chung của ba đường trung trực
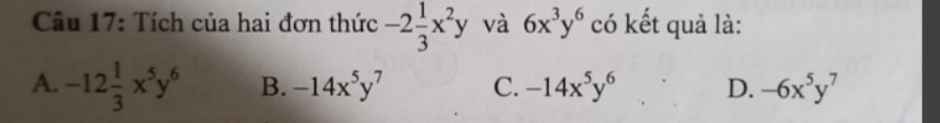








\(\left(-2\dfrac{1}{3}\right)x^2y\times6x^3y^6\)
\(=\left(-\dfrac{7}{3}\times6\right)x^5y^7\)
\(=-14x^5y^7\)
Chọn B
\(-2^1_3x^2y.6x^3y^6\)
\(=-14x^5y^7\)
Chọn B