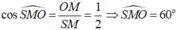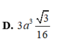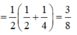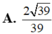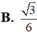Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
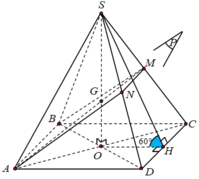
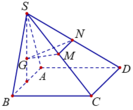
Gọi H là trung điểm cạnh CD và O là tâm hình vuông ABCD.
Ta có S. ABCD là hình chóp tứ giác đều nên các mặt bên hợp với đáy các góc bằng nhau
Giả sử S C D , A B C D ^ = S H O ^ = 60 o
Tam giác SHO vuông tại O có:
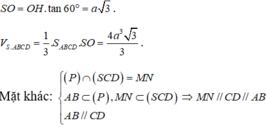
Mà G là trọng tâm tam giác SAC nên G cũng là trọng tâm tam giác SBD
Chọn A
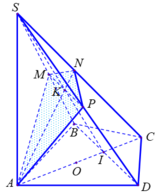
Gọi O là trọng tâm tam giác đều ABD và I là trung điểm BD thì:
Tam giác ICD vuông I có
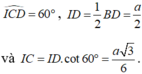
=> O và C đối xứng nhau qua đường thẳng BD
Tam giác SAC vuông tại A có SN. SC=SA²
Tam giác ABC có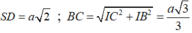 
và AC²=AB²+BC²
=> tam giác ABC vuông tại B 
Lại có tam giác SAB vuông nên 
M là trung điểm SB
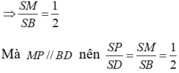
Mặt khác
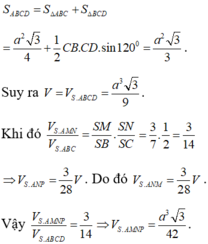
Chọn A.
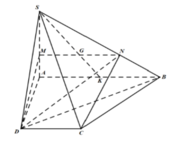
Gọi K là trung điểm của AB.
DC//AB => DC//(SAB)=> DC//MN
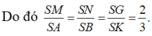
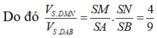
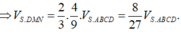
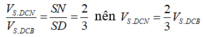
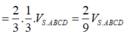
Do đó
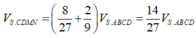
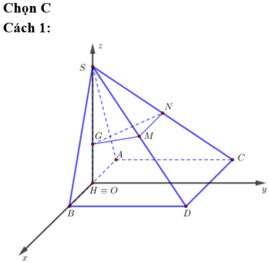
Chọn hệ trục tọa độ Oxyz như hình vẽ. Khi đó
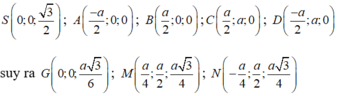
Ta có mặt phẳng (ABCD) có vectơ pháp tuyến là 
, mặt phẳng (GMN) có vectơ pháp tuyến là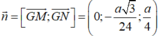 
Gọi (α) là góc giữa hai mặt phẳng (GMN) và (ABCD), ta có
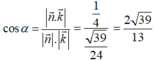
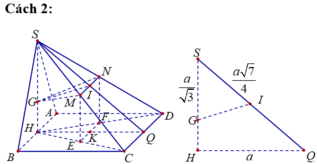
Gọi E, F lần lượt là hình chiếu của M và N lên (ABCD). Suy ra E, F lần lượt là trung điểm của HC, HD.
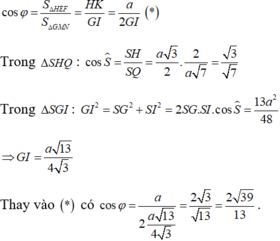
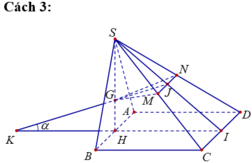
Gọi H, I lần lượt là trung điểm của AB, CD.
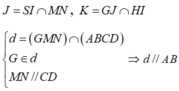
Mà d ⊥ (SIH) nên góc giữa góc giữa hai mặt phẳng (GMN) và (ABCD) là 
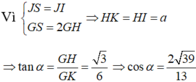
Đáp án B
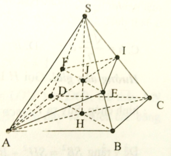
Do các cạnh bên bằng nhau nên hình chiếu của S lên (ABCD) phải trùng với tâm H của hình vuông ABCD.
Dễ thấy I là trung điểm của SC, vì BD ⊥ SC, nên BD//(P). Do đó EF // BD. Để ý rằng EF đi qua trọng tâm J của tam giác SDB.
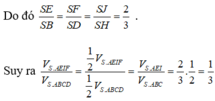
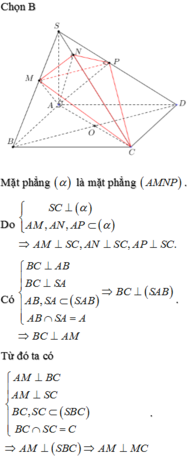
Chọn B
Ta có B C ⊥ S M . Gọi H là hình chiếu vuông góc của A trên SM. Do
và FE đi qua H.
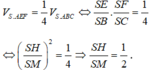
Vậy H là trung điểm cạnh SM. Suy ra tam giác SAM vuông cân tại A
⇒ S A = a 3 2 V S A B C = 1 3 . a 3 2 . a 2 3 4 = a 3 8
Chọn A
Gọi M là trung điểm CD. Góc tạo bởi mặt bên và mặt đáy là góc SMO
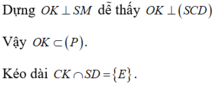
Đây là giao điểm cần tìm.
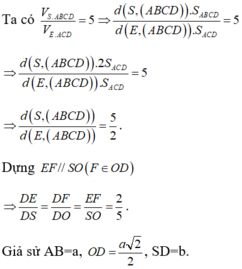
Xét tam giác vuông SOD.
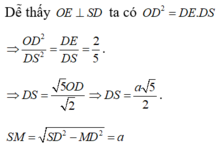
Xét tam giác vuông SOM vuông tại O có
