PD
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 12 2016
mình chỉ phân tích thôi
a) 6x(4-x)+x-4
=6x(4-x)-(4-x)
=(6x-1)(4-x)
c) 25x^2-10x+1-16z^2
=(5x-1)^2-16z^2
=(5x-1-4z)(5x-1+4z)
ban xem lại đề bài câu b đi chắc là sai đó
còn các câu trên bạn tự làm nhé
TK
17 tháng 12 2016
Thực hiện phép tính:
a) (2x-3y)(4x2+6xy+9y2)
=8x3-27y3
b) (6x3+3x2+4x+2):(3x2+2)
=(3x2+2)(2x+1):(3x2+2)
=2x+1
c) (x+2)2+(3-x)-2(x+3)(x-3)
=x2+4x+4+3-x-2x2+18
=-x2+4x+25
8 tháng 4 2022
Bài 2:
a: 6x(4-x)+(x-4)
=6x(4-x)-(4-x)
=(4-x)(6x-1)
b: \(=x^2-1+y\left(x^2-1\right)\)
\(=\left(x^2-1\right)\left(1+y\right)=\left(y+1\right)\left(x+1\right)\left(x-1\right)\)
c: \(=\left(5x-1\right)^2-\left(4z\right)^2\)
=(5x-1-4z)(5x-1+4z)
DH
1
30 tháng 7 2021
\(\frac{4}{x+2}+\frac{3}{x-2}+\frac{-5x-2}{x^2-4}\)ĐK : \(x\ne\pm2\)
\(=\frac{4\left(x-2\right)+3\left(x+2\right)-5x-2}{\left(x+2\right)\left(x-2\right)}=\frac{4x-8+3x+6-5x-2}{\left(x+2\right)\left(x-2\right)}\)
\(=\frac{2x-4}{\left(x+2\right)\left(x-2\right)}=\frac{2\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\frac{2}{x+2}\)
DH
2
AD
3 tháng 8 2021
\(\frac{\left(x-3\right)^3}{3x^2}:\frac{x^2-6x+9}{6x}\)
\(=\frac{\left(x-3\right)^3}{3x^2}.\frac{6x}{\left(x-3\right)^2}\)
\(=\frac{2\left(x-3\right)}{x}\)
\(=\frac{2x-6}{x}\)
#H
QA
3 tháng 8 2021
Trả lời:
\(\frac{\left(x-3\right)^3}{3x^2}:\frac{x^2-6x+9}{6x}\)
\(=\frac{\left(x-3\right)^3}{3x^2}.\frac{6x}{x^2-6x+9}\)
\(=\frac{\left(x-3\right)^3}{3x^2}.\frac{6x}{\left(x-3\right)^2}\)
\(=\frac{\left(x-3\right)^3.6x}{3x^2.\left(x-3\right)^2}\)
\(=\frac{2\left(x-3\right)}{x}\)
N
2
Y
4 tháng 1 2023
\(a,\dfrac{x+1}{5}-\dfrac{2}{x}\)
\(=\dfrac{x\left(x+1\right)-2.5}{5x}=\dfrac{x^2+x-10}{5x}\)
\(b,\dfrac{x+y}{9x}:\dfrac{x+y}{3x}\)
\(=\dfrac{x+y}{9x}.\dfrac{3x}{x+y}=\dfrac{1}{3}\)
4 tháng 1 2023
a. \(\dfrac{x+1}{5}\)-\(\dfrac{2}{x}\)=\(\dfrac{x\left(x+1\right)-2.5}{5x}\)=\(\dfrac{x^2+x-10}{5x}\)
b. \(\dfrac{x+y}{9x}:\dfrac{x+y}{3x}\)=\(\dfrac{x+y}{9x}.\dfrac{3x}{x+y}=\dfrac{1}{3}\)
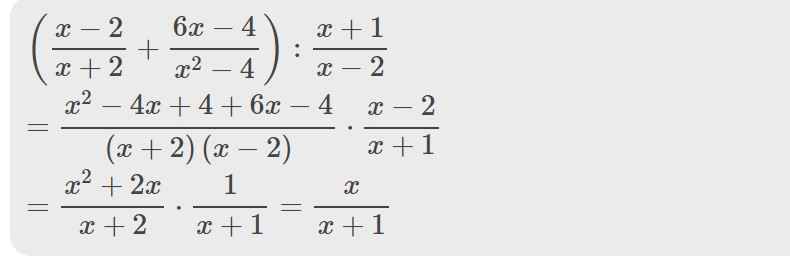
\(\left(\dfrac{x-2}{x+2}+\dfrac{6x-4}{x^2-4}\right):\dfrac{x+1}{x-2}\)
\(=\dfrac{x^2-4x+4+6x-4}{\left(x+2\right)\left(x-2\right)}\cdot\dfrac{x-2}{x+1}\)
\(=\dfrac{x^2+2x}{x+2}\cdot\dfrac{1}{x+1}=\dfrac{x}{x+1}\)