Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các đường thẳng HA, HB, HC lần lượt cắt cạnh đối BC, AC, AB tại N, M, E

a) ∆HBC có:
HN ⊥ BC nên HN là đường cao
BE ⊥ HC nên BE là đường cao
CM ⊥ BH nên CM là đường cao
Vậy A là trực tâm của ∆HBC
b) Tương tự trực tâm của ∆AHB là C, ∆AHC là B
Các đường thẳng HA, HB, HC lần lượt cắt cạnh đối BC, Ac, AB tại N, M, E.
a) ΔHBC có :
HN ⊥ BC nên HN là đường cao
BE ⊥ HC nên BE là đường cao
CM ⊥ BH nên CM là đường cao
Vậy A là trực tâm của ΔHBC.
b) Tương tự, trực tâm của ΔAHB là C; ΔAHC là B.

Giải
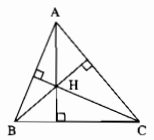
Trong ∆ABC ta có H là trực tâm nên
\(\text{ AH⊥BC,BH⊥AC,CH⊥AB}\)
Trong ∆AHB ta có:
\(\text{AC⊥BH }\)
\(\text{BC⊥AH}\)
Hai đường cao kẻ từ A và B cắt nhau tại C.
Vậy C là trực tâm của ∆AHB.
Trong ∆HAC ta có:
\(\text{BA⊥CH}\)
\(\text{CB⊥BH}\)
Hai đường cao kẻ từ A và C cắt nhau tại B, Vậy B là trực tâm của ∆HAC.
Trong ∆HBC ta có:
\(\text{BA⊥HC}\)
\(\text{CA⊥BH}\)
Hai đường cao kẻ từ B và C cắt nhau tại A. Vậy A là trực tâm của ∆HBC.

Tham khảo:
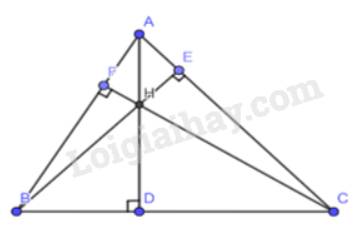
+) Xét tam giác HBC ta có :
HD vuông góc với BC \( \Rightarrow \) HD là đường cao tam giác HBC
BF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)BF là đường cao của tam giác HBC
CE vuông góc với HB tại E ( kéo dài HB ) \( \Rightarrow \)CE là đường cao của tam giác HBC
Ta kéo dài HD, BF, CE sẽ cắt nhau tại A
\( \Rightarrow \) A là trực tâm tam giác HBC
+) Xét tam giác HAB ta có :
HF vuông góc với AB \( \Rightarrow \) HF là đường cao tam giác HAB
BH vuông góc với AE tại E ( kéo dài HB ) \( \Rightarrow \)AE là đường cao của tam giác HAB
BD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)BD là đường cao của tam giác HAB
Ta kéo dài HF, BD, AE sẽ cắt nhau tại C
\( \Rightarrow \) C là trực tâm tam giác HAB
+) Xét tam giác HAC ta có :
HE vuông góc với AC \( \Rightarrow \) HE là đường cao tam giác HAC
AF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)AF là đường cao của tam giác HAC
CD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)CD là đường cao của tam giác HAC
Ta kéo dài CD, HE, AF sẽ cắt nhau tại B
\( \Rightarrow \) B là trực tâm tam giác HAC.

Các đường thẳng HA, HB, HC lần lượt cắt cạnh đối BC, AC, AB tại N, M, E
a) ∆HBC có:
HN ⊥ BC nên HN là đường cao
BE ⊥ HC nên BE là đường cao
CM ⊥ BH nên CM là đường cao
Vậy A là trực tâm của ∆HBC
b) Tương tự trực tâm của ∆AHB là C, ∆AHC là B

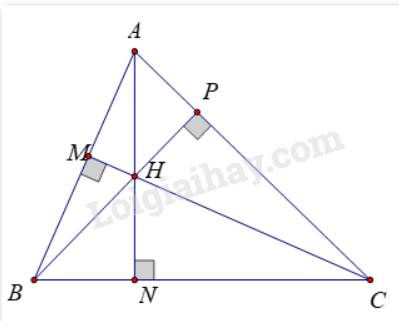
a)
Trong ΔABC ta có H là trực tâm nên:
AH ⊥ BC tại N, BH ⊥ AC tại P, CH ⊥ AB tại M
Trong ΔAHB, ta có:
HM ⊥ AB
BN ⊥ AH
Mà MH cắt BN tại C
=> C là trực tâm của tam giác AHB.
Trong ΔHAC, ta có:
HP ⊥ AC
CN ⊥ AH
Mà HP cắt CN tại B
=> B là trực tâm của ΔHAC.
Trong ΔHBC, ta có:
HN ⊥ BC
BM ⊥ HC
Mà HN cắt BM tại A
=> A là trực tâm của tam giác HBC.
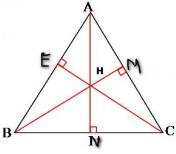
Chọn D