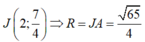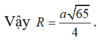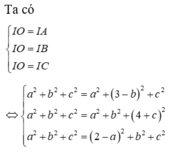Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Từ đề bài ta có \(A\left(n;0;0\right);B\left(0;m;0\right);C\left(0;0;1\right)\)
Gọi \(r\) là bán kính đường tròn ngoại tiếp tam giác vuông \(OAB\)
\(\Rightarrow r=\frac{AB}{2}=\frac{1}{2}\sqrt{m^2+n^2}\)
\(\Rightarrow R=\sqrt{\left(\frac{OC}{2}\right)^2+r^2}=\sqrt{\frac{1}{4}+\frac{1}{4}\left(m^2+n^2\right)}=\frac{1}{2}\sqrt{m^2+n^2+1}\)
Do \(m+2n=1\Rightarrow m=1-2n\)
\(\Rightarrow R=\frac{1}{2}\sqrt{\left(1-2n\right)^2+n^2+1}=\frac{1}{2}\sqrt{5n^2-4n+2}\)
\(\Rightarrow R=\frac{1}{2}\sqrt{5\left(n-\frac{2}{5}\right)^2+\frac{6}{5}}\ge\frac{1}{2}\sqrt{\frac{6}{5}}\)
\(\Rightarrow R_{min}=\frac{1}{2}\sqrt{\frac{6}{5}}=\frac{\sqrt{30}}{10}\) khi \(n=\frac{2}{5}\Rightarrow m=\frac{1}{5}\Rightarrow2m+n=\frac{4}{5}\)
Chọn A
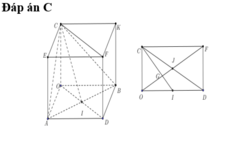
Gọi I (a;b;c)
Ta có IA=IO=R ó hình chiếu của I lên OA là trung điểm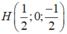 
của OA.
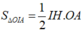
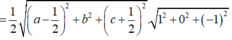
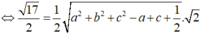
Theo bài ra ta có:
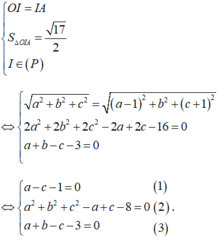
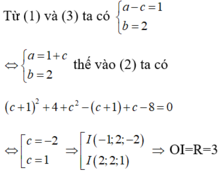
Đáp án A
Phương pháp giải: Xác định tọa độ ba điểm A, B, C và gọi tâm I, sử dụng điều kiện cách đều IA=IB=IC=IO để tìm tọa độ tâm I của mặt cầu
Lời giải:
Gọi A(a;0;0), B(0;b;0), C(0;0;c) => Tọa độ trọng tâm G là
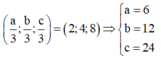
Gọi tâm mặt cầu (S) là I(x;y;z) => IO =IA = IB =IC
Vậy tọa độ tâm mặt cầu là I(3;6;12)
Chọn A
Điểm M(1;0;0) là 1 điểm thuộc (P)
Vì (P) // (Q) nên
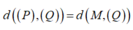
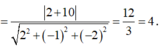
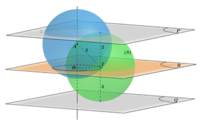
Giả sử I(a;b;c) là tâm của (S). Vì (S) tiếp xúc với cả (P) và (Q) nên bán kính mặt cầu (S) là:
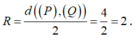
Do đó IA = 2 nên I luôn thuộc mặt cầu (T) tâm A, bán kính 2.
Ngoài ra
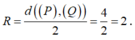
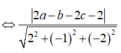
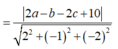
Do đó I luôn thuộc mặt phẳng (R): 2x-y-2z+4=0.
Gọi H là hình chiếu vuông góc của A lên (R). Vì A, (R) cố định nên H cố định.
Ta có
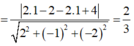
do đó tam giác AHI vuông tại H nên
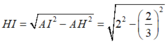
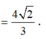
Vậy I luôn thuộc đường tròn tâm H, nằm trên mặt phẳng (R), bán kính
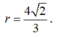
Đáp án D.
Mặt cầu tiếp xúc với cả ba mặt cầu trên là mặt cầu tiếp xúc ngoài với cả 3 mặt cầu trên. Gọi I là tâm và R là bán kính mặt cầu cần tìm
Ta có:
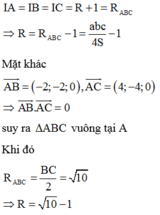
Đáp án là A
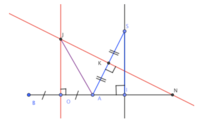
* Gọi J là tâm mặt cầu qua đường tròn tâm O và điểm S => J nằm trên đường trung trực của AB và SA
*Tam giác SIA vuông tại I.
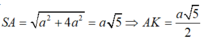
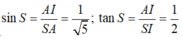
*Ta có: Góc N và S bằng nhau vì cùng phụ với góc S A N ^
* Tam giác AKN vuông tại K
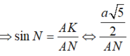
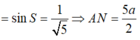
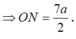
* Tam giác OJN vuông tại O
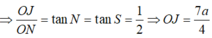
* Tam giác AOJ vuông tại O
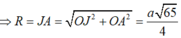
Cách 2
Gắn hệ trục toạ độ Oxy sao cho A, B, O thuộc tia Ox, S thuộc tia Oy và giả sử a = 1.
Khi đó A(1;0), B(3;0), S(0;2)
là đường tròn tâm J qua 3 điểm A, S, B
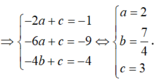
Suy ra:
