Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Tổng số người tăng lên trong năm 2027 là: 1,5(1+1,5%)10 - 1,5(1+1,5%)9 = 25726 người.
Số dân tăng lên này bằng số người sinh ra trừ số người tử vong năm 2027
Do đó trong năm 2027 có 25723 + 2700 = 28426 người.

Ta có: \({u_1} = 3,\;q = 1- 0,2 = 0,8\).
Giá trị của máy ủi sau n năm là: \({u_n} = 3 \times {0,8^{n - 1}}\)
Vậy sau 5 năm sử dụng giá trị của máy ủi là: \({u_5} = 3 \times {0,8^{5 - 1}} = 1,2288\) (tỷ đồng)

Lập phương trình
Gọi số trang là: x {hỏi cái gì đắt cái đó làm ẩn}
gọi số trang đọc theo đọc được theo từng ngày là: a[1,2,3]
thì ta có hệ phương trình:\(\left\{\begin{matrix}a_1+5=\frac{1}{5}x\\a_2-7=\left(x-a_1\right)\\a_3=\frac{2}{5}\left[x-\left(a_1+a_2\right)\right]\\a_4=\frac{2}{3}\left[x-\left(a_1+a_2+a_3\right)\right]\end{matrix}\right.\)
Thiếu 1 pt: \(\left(a_1+a_2+a_3+a_4+41\right)=x\) {không vào sửa được-> viết ngoài hệ}
Như vậy ta có hệ 5 pt 5 ẩn => đủ để tìm x, (bạn tự làm)
đọc lại đề nhầm ngày thứ 4 đọc hết quyển truyện {tương còn để lại 41}
do vây--> a4=2/3[...]+41
Phuowfg trình bên ngoài hệ còn (a1+a2+a3+a4)=x

Theo phương án 1, tiền lương mỗi quý tạo thành cấp số nhân với
\({u_1} = 5 \times 3 = 15\), công sai \(d = 0,5 \times 3 = 1,5\)
Công thức tổng quát \({u_n} = 15 + 1,5\left( {n - 1} \right)\)
Sau 3 năm làm việc \(\left( {n = 12} \right)\), lương của người nông dân là:
\(\frac{{12}}{2}\left[ {2 \times 15 + \left( {12 - 1} \right) \times 1,5} \right] = 279\) (triệu đồng)
Theo phương án 2, tiền lương mỗi quý sẽ tạo thành cấp số nhân với
\({u_1} = 5 \times 3 = 15\), công bội \(q = 1,05\)
Công thức tổng quát \({u_n} = 15 \times 1,{05^{n - 1}}\)
Sau 3 năm làm việc \(\left( {n = 12} \right),\) lương của người nông dân là:
\(\frac{{15\left( {1 - 1,{{05}^{12}}} \right)}}{{1 - 1,05}} = 238,757\) (triệu đồng)
Vậy thì theo phương án 1 thì tổng lương nhận được của người nông dân cao hơn.

Số tiền lương anh Nam nhận được sau 10 lập thành cấp số cộng với:
Số hạng đầu \({u_1} = 100\) và công sai \(d = 20\)
Tổng lương anh Nam nhận được sau 10 năm là:
\({S_n} = \frac{n}{2}\left[ {2{u_1} + \left( {n - 1} \right)d} \right] = \frac{{10}}{2}\left[ {2.100 + \left( {10 - 1} \right).20} \right] = 1900\) (triệu đồng)

a)
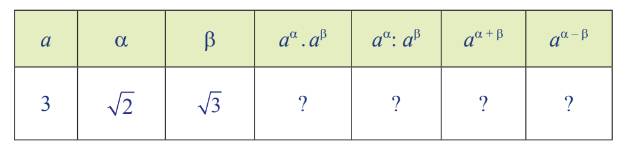
| a | α | b | \(a^{\alpha}\cdot a^{\beta}\) | \(a^{\alpha}:a^{\beta}\) | \(a^{\alpha+\beta}\) | \(\alpha^{\alpha+\beta}\) |
| 3 | \(\sqrt{2}\) | \(\sqrt{3}\) | \(3^{\sqrt{2}}\cdot3^{\sqrt{3}}=31,70659\) | \(3^{\sqrt{2}}:3^{\sqrt{3}}=0,70527\) | \(3^{\sqrt{2}+\sqrt{3}}=31,70659\) | \(3^{\sqrt{2}-\sqrt{3}}=0,70527\) |
b) Nhận xét:
\(a^m\cdot a^n=a^{m+n};a^m:a^n=a^{m-n}\)

Tham khảo:
a)

b) Với mẫu số liệu không ghép nhóm:
\(\bar x = \left( {5 + 3 + 10 + 20 + 25 + 11 + 13 + 7 + 12 + 31 + 19 + 10 + 12 + 17 + 18 + 11 + 32 + 17 + 16 + 2 + 7 + 9 + 7 + 8 + 3 + 5 + 12 + 15 + 18 + 3 + 12 + 14 + 2 + 9 + 6 + 15 + 15 + 7 + 6 + 12} \right):40 = 11.9\)
Với mẫu số liệu ghép nhóm:
\(\bar x = \frac{{2.5 \times 6 + 7.5 \times 10 + 12.5 \times 11 + 17.5 \times 9 + 22.5 + 27.5 + 32.5 \times 2}}{{40}} = 12.5\).
Số trung bình của mẫu số liệu không ghép nhóm chính xác hơn.
c) 11 là tần số lớn nhất nên nhóm chưa mốt là \(\left[ {10;15} \right)\).