Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: \(A=10x^2+20xy+10y^2-90\)
\(=10\left(x^2+2xy+y^2-9\right)\)
\(=10\left(x+y-3\right)\left(x+y+3\right)\)
b: Ta có: \(B=x^3y-3x^2y-4xy+12y\)
\(=x^2y\left(x-3\right)-4y\left(x-3\right)\)
\(=y\left(x-3\right)\left(x-2\right)\left(x+2\right)\)
c: Ta có: \(C=125x^3-10x^2+2x-1\)
\(=\left(5x-1\right)\left(25x^2+5x+1\right)-2x\left(5x-1\right)\)
\(=\left(5x-1\right)\left(25x^2+3x+1\right)\)

\(A=25x^2-20x+7\)
\(\Leftrightarrow A=\left(5x-2\right)^2+3\ge3\)
Dấu " = " xảy ra \(\Leftrightarrow5x-2=0\Leftrightarrow x=\frac{2}{5}\)
Vậy \(minA=3\Leftrightarrow x=\frac{2}{5}\)
\(B=-x^2+2x-2\)
\(\Leftrightarrow B=-\left(x^2-2x+1\right)-3\)
\(\Leftrightarrow B=-\left(x-1\right)^2-3\le-3\)
Dấu " = " xảy ra \(\Leftrightarrow x=1\)
Vậy \(maxB=-3\Leftrightarrow x=1\)
\(C=9x^2-12x\)
\(\Leftrightarrow C=\left(9x^2-12x+4\right)-4\)
\(\Leftrightarrow C=\left(3x-2\right)^2-4\ge-4\)
Dấu " = " xảy ra \(\Leftrightarrow3x-2=0\Leftrightarrow x=\frac{2}{3}\)
Vậy \(minC=-4\Leftrightarrow x=\frac{2}{3}\)
\(D=3-10x^2-4xy-4y^2\)
\(\Leftrightarrow D=-\left(4y^2+4xy+x^2+9x^2\right)-3\)
\(\Leftrightarrow D=-\left[\left(2y-x\right)^2+3x^2\right]-3\le-3\)
Dấu " = " xảy ra \(\Leftrightarrow\hept{\begin{cases}2y-x=0\\3x^2=0\end{cases}\Leftrightarrow}\hept{\begin{cases}y=0\\x=0\end{cases}}\)
Vậy \(maxD=-3\Leftrightarrow x=y=0\)
\(E=4x-x^2+1\)
\(\Leftrightarrow E=-\left(x^2-4x+4\right)+5\)
\(\Leftrightarrow E=-\left(x-2\right)^2+5\le5\)
Dấu " = " xảy ra \(\Leftrightarrow x=2\)
Vậy \(maxE=5\Leftrightarrow x=2\)

a: \(6x^2-3x\)
\(=3x\cdot2x-3x\)
=3x(2x-1)
b: \(15x^5y^4+10x^3y^3-5xy\)
\(=5xy\cdot3x^4y^3+5xy\cdot2x^2y^2-5xy\cdot1\)
\(=5xy\left(3x^4y^3+2x^2y^2-1\right)\)
c: \(x^2y+4xy+4y\)
\(=y\cdot x^2+y\cdot4x+y\cdot4\)
\(=y\left(x^2+4x+4\right)=y\left(x+2\right)^2\)

\(\frac{x^2+3xy+2y^2}{5x^2+4xy-y^2}-\frac{x^2-5xy+4y^2}{-2x^2+4xy-2y^2}\)
\(=\frac{x+2y}{5x-y}-\left[-\frac{x-4y}{2\left(x-y\right)}\right]\)
\(=\frac{x+2y}{5x-y}+\frac{x-4y}{2\left(x-y\right)}\)
\(=\frac{\left(x+2y\right).2\left(x-y\right)}{\left(5x-y\right).2\left(x-y\right)}+\frac{\left(x-4y\right).\left(5x-y\right)}{2\left(x-y\right).\left(5x-y\right)}\)
\(=\frac{\left(x+2y\right).2\left(x-y\right)+\left(x-4y\right).\left(5x-y\right)}{2\left(x-y\right).\left(5x-y\right)}\)
\(=\frac{7x^2-19xy}{2\left(x-y\right).\left(5x-y\right)}\)

Bài 1 :
a ) \(x^2-6x-y^2+9=\left(x^2-6x+9\right)-y^2=\left(x-3\right)^2-y^2=\left(x-3+y\right)\left(x-3-y\right)\)
b) \(25-4x^2-4xy-y^2=5^2-\left(4x^2+4xy+y^2\right)=5^2-\left(2x+y\right)^2=\left(5+2x+y\right)\left(5-2x-y\right)\)
c) \(x^2+2xy+y^2-xz-yz=\left(x+y\right)^2-z.\left(x+y\right)=\left(x+y\right)\left(x+y-z\right)\)
d) \(x^2-4xy+4y^2-z^2+4tz-4t^2=\left(x^2-4xy+4y^2\right)-\left(z^2-4tz+4t^2\right)\)
\(=\left(x-2y\right)^2-\left(z-2t\right)^2=\left(x-2y+z-2t\right).\left(x-2y-z+2t\right)\)
BÀi 2 :
a) \(ax^2+cx^2-ay+ay^2-cy+cy^2=\left(ax^2+cx^2\right)-\left(ay+cy\right)+\left(ay^2+cy^2\right)\)
\(=x^2.\left(a+c\right)-y\left(a+c\right)+y^2.\left(a+c\right)=\left(a+c\right).\left(x^2-y+y^2\right)\)
b) \(ax^2+ay^2-bx^2-by^2+b-a=\left(ax^2-bx^2\right)+\left(ay^2-by^2\right)-\left(a-b\right)\)
\(=x^2.\left(a-b\right)+y^2.\left(a-b\right)-\left(a-b\right)=\left(a-b\right)\left(x^2+y^2-1\right)\)
c) \(ac^2-ad-bc^2+cd+bd-c^3=\left(ac^2-ad\right)+\left(cd+bd\right)-\left(bc^2+c^3\right)\)
\(=-a.\left(d-c^2\right)+d.\left(b+c\right)-c^2.\left(b+c\right)=\left(b+c\right).\left(d-c^2\right)-a\left(d-c^2\right)\)
\(=\left(b+c-a\right)\left(d-c^2\right)\)
BÀi 3 :
a) \(x.\left(x-5\right)-4x+20=0\) \(\Leftrightarrow x\left(x-5\right)-4\left(x-5\right)=0\) \(\Leftrightarrow\left(x-5\right)\left(x-4\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x-5=0\\x-4=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=5\\x=4\end{cases}}}\)
b) \(x.\left(x+6\right)-7x-42=0\)\(\Leftrightarrow x.\left(x+6\right)-7.\left(x+6\right)=0\) \(\Leftrightarrow\left(x+6\right)\left(x-7\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x+6=0\\x-7=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=-6\\x=7\end{cases}}}\)
c) \(x^3-5x^2+x-5=0\) \(\Leftrightarrow x^2.\left(x-5\right)+\left(x-5\right)=0\) \(\Leftrightarrow\left(x-5\right)\left(x^2+1\right)\)
\(\Leftrightarrow\hept{\begin{cases}x^2+1=0\\x-5=0\end{cases}\Leftrightarrow\hept{\begin{cases}x^2=-1\left(KTM\right)\\x=5\end{cases}}}\)
d) \(x^4-2x^3+10x^2-20x=0\) \(\Leftrightarrow x.\left(x^3-2x^2+10x-20\right)=0\)\(\Leftrightarrow x.\left[x^2.\left(x-2\right)+10.\left(x-2\right)\right]=0\) \(\Leftrightarrow x.\left(x-2\right)\left(x^2+10=0\right)\)
\(\Leftrightarrow\hept{\begin{cases}x=0\\x-2=0\\x^2+10=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\\x=2\\x^2=-10\left(KTM\right)\end{cases}}}\)

a, \(=12x^5+9x^3y^2-6x^2y^3-20x^4y-15x^2y^3-10xy^4-24x^3y^2-18xy^4+12y^5\)
(tự rút gọn cái :P)
b, \(8x^3+4x^2y-2xy^2-y^3\)
\(=4x^2\left(2x+y\right)-y^2\left(2x+y\right)=\left(2x+y\right)^2\left(2x-y\right)\)
\(4x^2y^2-4x^2-4xy-y^2=4x^2y^2-\left(2x+y\right)^2\)
\(=\left(2x+y+2xy\right)\left(2xy-2x+y\right)\)
Mấy cái còn lại nhân tung ra là được mà :))))
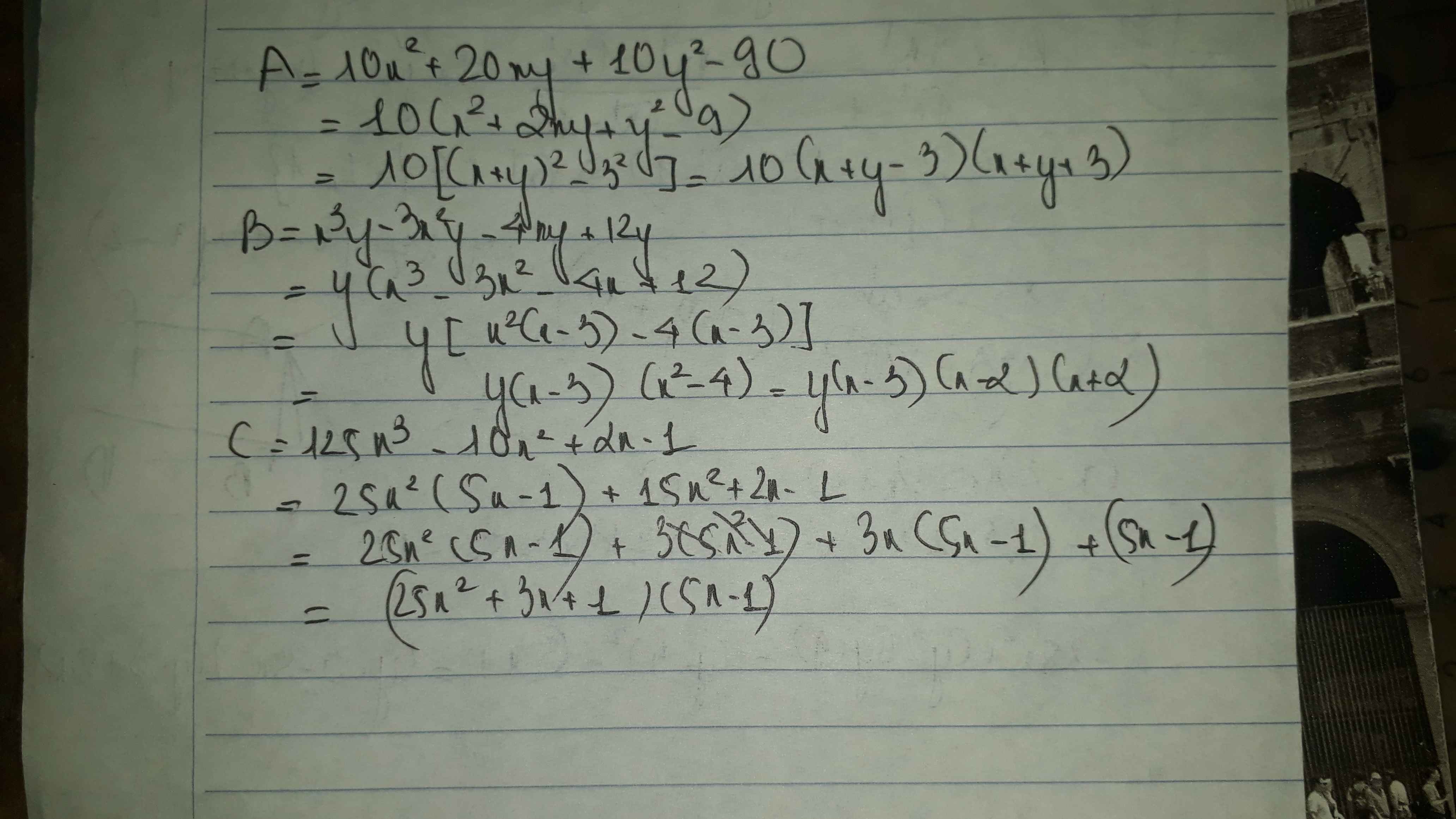
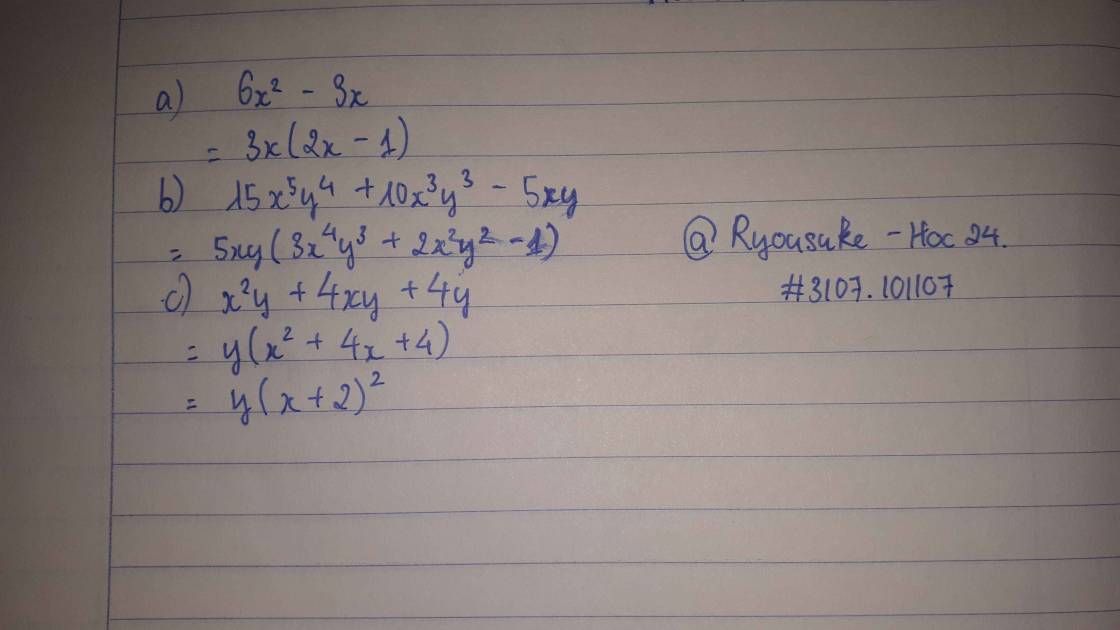
A
Chọn A