Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
Thể tích vật thể được sinh ra khi
cho hình phẳng giới hạn bởi các đường
![]()
![]()
Cách giải:
Thể tích cần tìm là
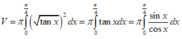
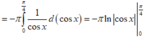
![]()
Chọn A.

1.
\(V=\pi\int\limits^1_0x^6dx=\dfrac{\pi x^7}{7}|^1_0=\dfrac{\pi}{7}\)
2.
\(F\left(x\right)=\int sin2xdx=-\dfrac{1}{2}cos2x+C\)
\(f\left(\dfrac{\pi}{4}\right)=1\Leftrightarrow-\dfrac{1}{2}cos\dfrac{\pi}{2}+C=1\Rightarrow C=1\)
\(\Rightarrow F\left(x\right)=-\dfrac{1}{2}cos2x+1\Rightarrow F\left(\dfrac{\pi}{6}\right)=\dfrac{3}{4}\)

Chọn D
D quay xung quanh trục Oy
Ta có: y = ( x - 2 ) 2 ⇔ x - 2 = ± y ⇔ x = 2 ± y
V = π ∫ 0 4 2 + y 2 - 2 - y 2 dy = 8 π . ∫ 0 4 y dy = 8 π . 2 3 y 3 2 | 0 π = 128 π 3 đ v t t
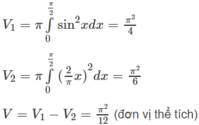
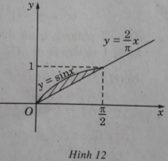
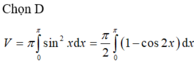

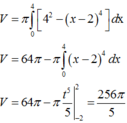
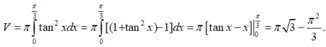
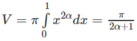
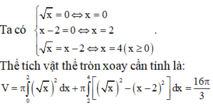
Câu 1: pt hoành độ giao điểm: \(x^2-4x+3=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
Diện tích hình phẳng:
\(S=\int\limits^3_1\left(-x^2+4x-3\right)dx=\frac{4}{3}\)
Câu 2:
Thể tích: \(V=\pi\int\limits^{\frac{\pi}{4}}_0tan^2xdx=\pi\int\limits^{\frac{\pi}{4}}_0\left(\frac{1-cos^2x}{cos^2x}\right)dx=\pi\int\limits^{\frac{\pi}{4}}_0\left(\frac{1}{cos^2x}-1\right)dx\)
\(=\pi\left(tanx-x\right)|^{\frac{\pi}{4}}_0=\pi\left(1-\frac{\pi}{4}\right)\)