Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên
AH ⊥ BC và HB = HC
Xét hai tam giác vuông HAB và HAC có:
HB = HC
= 900
AH: cạnh chung
Nên ∆HAB = ∆HAC => AB = AC
Vậy ∆ABC cân tại A
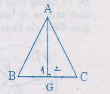
xét tam giác AMB và tam giác AMC, có:
AB=AC
MB=MC(gt)
AM chung
=>tam giác AMB= tam giác AMC (c.c.c)
M1=M2 mà góc M1+góc M2=180 độ
=>góc M1= góc M2= góc MC=90 độ
=>AM vuông góc với BC
mà MA=MB
=>AM là đường trung trực của tam giác ABC
Yên tâm đi chắc chắn đúng

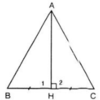
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên AH ⊥ BC và HB = HC
Xét hai tam giác vuông HAB và HAC, có:
HB = HC
AH: cạnh chung
Nên ∆HAB = ∆HAC (hai cạnh góc vuông)
⇒ AB = AC (hai cạnh tương ứng)
Vậy ∆ABC cân tại A.

Hướng dẫn:
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên
AH ⊥ BC và HB = HC
Xét hai tam giác vuông HAB và HAC có:
HB = HC
ˆH1=ˆH2H1^=H2^ = 900
AH: cạnh chung
Nên ∆HAB = ∆HAC => AB = AC
Vậy ∆ABC cân tại A
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên
AH ⊥ BC và HB = HC

Xét hai tam giác vuông HAB và HAC có:
HB = HC
ˆH1=ˆH2H1^=H2^ = 900
AH: cạnh chung
Nên ∆HAB = ∆HAC => AB = AC
Vậy ∆ABC cân tại A

- Giả sử AD vừa là đường trung tuyến, vừa là đường phân giác của tam giác ABC.
Ta cần chứng minh ∆ABC cân tại A.
Kéo dài AD một đoạn DA1 sao cho DA1 = AD.
- ∆ADB và ∆A1DC có
AD = DA1 (cách vẽ)
BD = CD (do D là trung điểm BC)
Giải bài 42 trang 73 SGK Toán 7 Tập 2 | Giải toán lớp 7
⇒ ∆ADB = ∆A1DC (c.g.c)
⇒ Giải bài 42 trang 73 SGK Toán 7 Tập 2 | Giải toán lớp 7 (hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
Giải bài 42 trang 73 SGK Toán 7 Tập 2 | Giải toán lớp 7
⇒ ∆ACA1 cân tại C ⇒ AC = A1C (2)
Từ (1) và (2) ⇒ AB = AC.
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.

- Giả sử AD vừa là đường trung tuyến, vừa là đường phân giác của tam giác ABC.
Ta cần chứng minh ∆ABC cân tại A.
Kéo dài AD một đoạn DA1 sao cho DA1 = AD.
- ∆ADB và ∆A1DC có
AD = DA1 (cách vẽ)
BD = CD (do D là trung điểm BC)
⇒ ∆ADB = ∆A1DC (c.g.c)
⇒ 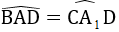
⇒ ∆ACA1 cân tại C ⇒ AC = A1C (2)
Từ (1) và (2) ⇒ AB = AC.
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.
HOK T ~

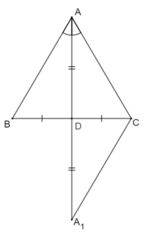
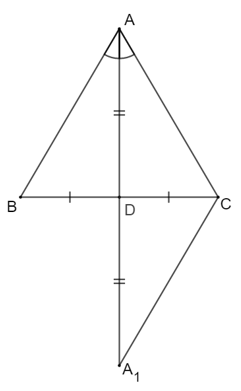
- Giả sử AD vừa là đường trung tuyến, vừa là đường phân giác của tam giác ABC.
Ta cần chứng minh ∆ABC cân tại A.
Kéo dài AD một đoạn DA1 sao cho DA1 = AD.
- ∆ADB và ∆A1DC có
AD = DA1 (cách vẽ)
BD = CD (do D là trung điểm BC)

⇒ ∆ADB = ∆A1DC (c.g.c)
⇒ 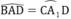 (hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
(hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
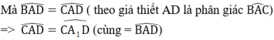
⇒ ∆ACA1 cân tại C ⇒ AC = A1C (2)
Từ (1) và (2) ⇒ AB = AC.
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.
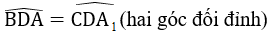
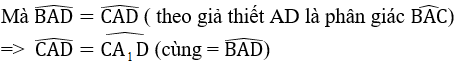
Dựa vào sách giáo khoa ý
A B C D Cả 4 câu đều là 1 hình như thế này, chỉ có kí hiệu khác nhau, bạn tự dựa vào nội dung câu hỏi mà kí hiệu lên hình nhé.
Câu 1:
Xét tam giác ABD và tam giác ACD:
ADB= ADC =90o
AD chung
DB= DC
=> tam giác ABD = tam giác ACD (2 cạnh góc vuông)
=> góc B = góc C (2 góc tương ứng)
Vậy tam giác ABC cân
Câu 2:
Chứng minh y chang câu 1
Câu 3:
Xét tam giác ABD và tam giác ACD:
ADB= ADC =90o
AD chung
BAD = CAD
=> tam giác ABD = tam giác ACD (cạnh góc vuông_ góc nhọn)
=> góc B = góc C (2 góc tương ứng)
Vậy tam giác ABC cân
Câu 4:
Chứng minh giống hệt câu 3.