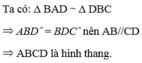Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

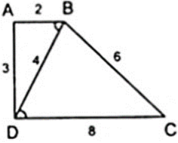
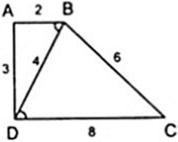
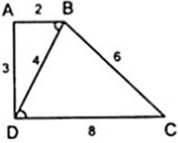
Ta có: Δ BAD ∼ Δ DBC
⇒ A B D ^ = B D C ^ nên AB//CD
⇒ ABCD là hình thang.

Ta có:
BA/BD = AD/BC = BD/CD = 1/2 ⇒ Δ BAD ∼ Δ DBC ( c - c - c )

Ta có:
BA/BD = AD/BC = BD/CD = 1/2 ⇒ Δ BAD ∼ Δ DBC ( c - c - c )

Bài 3: Xét tam giác BCD có :
BC=DC ( gt )
-> tam giác BCD cân tại C
-> ^B1 = ^D1 ( 2 góc đáy )(1)
Mặt khác : BD là tia phân giác của ^D
-> ^D1 =^D2 (2)
Từ (1) và (2) suy ra : ^B1 = ^D2 ( cùng = ^D1 )
-> BC // DA ( có cặp góc so le trong = nhau )
-> Tứ giác ABCD là hình thang ( có 2 cạnh đối song song )
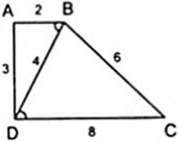
Bài 4 : Từ B hạ BH vuông góc với DC (1)
Do tứ giác ABCD có ^A=^D = 900 ( gt)(2)
Từ (1) và (2) suy ra : Tứ giác ABCD là HCN ( dấu hiệu nhận biết )
-> DH = AB =2 cm ( 2 cạnh đối )
BH = AD= 2 cm ( 2 cạnh đối)
Mà DH +HC = DC= 4 (cm) ( gt)
-> HC = 2 ( cm)
Áp dụng định lí Py ta go trong tam giác vuông BHC có :
BH2 + HC2 = BC2
-> 22 + 22 = BC2
Vậy BC = \(\sqrt{8}\)(cm)
hình vẽ chỉ minh họa thôi bạn mà vẽ thì vẽ số liệu chính xác hơn nha !
Ở bài 4 có thể chứng minh tứ giác đó là hình vuông nhá bạn

a)Vẽ ∆DBC biết BD = 5 cm, BC = 10 cm, DC = 12,5 cm.
Trên nửa mặt phẳng bờ BD không chứa C vẽ hai cung tròn tâm B và tâm D bán kính lần lượt là 4 cm và 8 cm. Hai cung này cắt nhau tại A.
Vẽ các đoạn BA, DA được tứ giác ABCD.
ABBD=410=25;BDDC=1025=25;ADBC=820=25ABBD=410=25;BDDC=1025=25;ADBC=820=25
=>ABBD=BDDC=ADBC=>ΔABDΔBDCABBD=BDDC=ADBC=>ΔABDΔBDC
∆ABD∽ ∆BDC =>ˆABD=ˆBDCABD^=BDC^ lại so le trong.
=>AB // DC hay ABCD là hình thang.

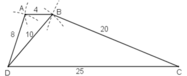
a) Cách vẽ:
- Vẽ ΔBDC:
+ Vẽ DC = 25cm
+ Vẽ cung tròn tâm D có bán kính = 10cm và cung tròn tâm C có bán kính = 20cm. Giao điểm của hai cung tròn là điểm B.
Nối DB và BC.
- Vẽ điểm A: Vẽ cung tròn tâm B có bán kính = 4cm và cung tròn tâm D có bán kính = 8cm. Giao điểm của hai cung tròn này là điểm A.
Nối DA và BA.
Vậy là ta đã vẽ được tứ giác ABCD thỏa mãn điều kiện đề bài.