Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

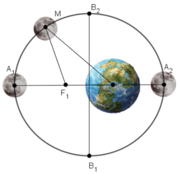
Theo đề bài có:
Độ dài trục lớn của elip bằng 769266km ⇒ A1A2 = 2a = 769266 ⇒ a = 384633
Độ dài trục nhỏ của elip bằng 768106km ⇒ B1B2 = 2b = 768106 ⇒ b = 384053
⇒ c2 = a2 – b2 = 445837880 ⇒ c ≈ 21115
⇒ F1F2 = 2c = 42230
⇒ A1F1 = A2F2 = (A1A2 – F1F2)/2 = 363518
+ Trái Đất gần Mặt Trăng nhất khi Mặt Trăng ở điểm A2
⇒ khoảng cách ngắn nhất giữa Trái Đất và Mặt Trăng bằng A2F2 = 363518 km
+ Trái Đất xa Mặt Trăng nhất khi Mặt Trăng ở điểm A1
⇒ khoảng cách xa nhất giữa Trái Đất và Mặt Trăng bằng:
A1F2 = A1F1 + F1F2 = 405748 km.

Ta có:
\({A_1}{A_2} = 2a \Rightarrow 2a = 768800 \Rightarrow a = 384400\) và \({B_1}{B_2} = 2b \Rightarrow 767619 = 2b \Rightarrow b = 383809,5\)
Vậy phương trình chính tắc của (E) là: \(\frac{{{x^2}}}{{{{384400}^2}}} + \frac{{{y^2}}}{{383809,5}^2} = 1\)

Gắn hệ trục Oxy vào chiếc cổng, gọi chiều cao của cổng là h ta vẽ lại parabol như dưới đây:
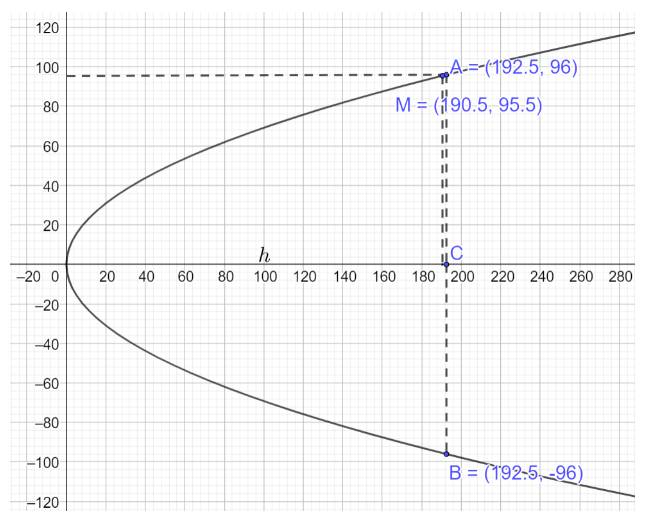
Phương trình parabol mô phỏng cổng có dạng \({y^2} = 2px\)
Theo giả thiết \(AB = 2{y_A} = 192 \Rightarrow {y_A} = 96,OC = h \Rightarrow M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\)
Thay tọa độ các điểm \(M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\) vào phương trình \({y^2} = 2px\) ta có:
\(\left\{ \begin{array}{l}95,{5^2} = 2p\left( {h - 2} \right)\\{96^2} = 2ph\end{array} \right. \Rightarrow \left\{ \begin{array}{l}p = \frac{{383}}{{16}}\\h \simeq 192,5\end{array} \right.\)
Vậy chiều cao của cổng gần bằng 192,5 m

Phép đo của các nhà thiên văn có sai số tuyệt đối không vượt quá \(\frac{1}{4}\) ngày, có nghĩa là không vượt quá 360 phút. Phép đo của Hùng có sai số tuyệt đối không vượt quá 1 phút. Nếu chỉ so sánh 360 phút và 1 phút thì có thể dẫn đến hiểu rằng phép đo của bạn Hùng chính xác hơn phép đo của các nhà thiên văn. Tuy nhiên, \(\frac{1}{4}\) ngày hay 360 phút là độ chính xác của phép đo một chuyển động trong 365 ngày, còn 1 phút là độ chính xác của phép đo một chuyển động trong 15 phút. So sánh hai tỉ số \(\frac{{\frac{1}{4}}}{{365}} = \frac{1}{{1460}} = 0,0006849...\) và\(\frac{1}{{15}} = 0,0666...\) , ta thấy rằng phép đo của các nhà thiên văn chính xác hơn nhiều.

1 mặt trời được hình thành từ lava và thiên thạch
2 muốn bt mặt trời nặng bao nhiêu thì mẹ hãy cho con bt cân nặng của trái đất và con người
3 có hoặc ko
4 có số miệng núi lửa bằng số cây trên trái đất
5 vì áp suất của ngoài vũ trụ chỉ cho phép toàn bộ hình tròn
6 có vì các điều đó đều là sự thật
7 trái đất được tạo từ thiên thạch
8 vì trái đất là một hành tinh đặc bt như mẹ vậy
9 vậy con người hãy ngừng hoạt động các nhà máy
10 vì thiên nhiên giúp ta có thể sống , thở,....
mọi người có lắng nghe được vì mọi tiếng ồn của tự nhiên đều là lời nói của thiên nhiên

a: Gọi hàm số bậc hai cần tìm là (P): \(y=ax^2+bx+c\)
Thay x=0 và y=-7 vào (P), ta được:
\(a\cdot0^2+b\cdot0+c=-7\)
=>c=-7
=>(P): \(y=ax^2+bx-7\)
Thay x=-4 và y=10 vào (P), ta được: \(a\cdot\left(-4\right)^2+b\cdot\left(-4\right)-7=10\)
=>16a-4b=17(1)
Thay x=20 và y=5 vào (P), ta được:
\(a\cdot20^2+b\cdot20-7=5\)
=>400a+20b=12(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}16a-4b=17\\400a+20b=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}80a-20b=85\\400a+20b=12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}480a=97\\16a-4b=17\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{97}{480}\\4b=16a-17=-\dfrac{413}{30}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=\dfrac{97}{480}\\b=-\dfrac{413}{120}\end{matrix}\right.\)
Vậy: (P): \(y=\dfrac{97}{480}x^2-\dfrac{413}{120}x-7\)

a) Khi cân một túi gạo thì ta kết quả là một số gần đúng vì đây là một cách đo đạc.
b) Ta không biết chính xác bán kính Trái Đất nên 6 371 cũng là số gần đúng.
c) Trái Đất quay một vòng quanh Mặt Trời mất 365 ngày cũng là số gần đúng.