
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{99.101}\)
\(=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{99}-\frac{1}{101}\)
\(=1-\frac{1}{101}=\frac{100}{101}\)
b) \(\frac{4}{3.5}+\frac{4}{5.7}+\frac{4}{7.9}+...+\frac{4}{97.99}\)
\(=2\left(\frac{2}{3.5}+\frac{2}{5.7}+\frac{2}{7.9}+...+\frac{2}{97.99}\right)\)
\(=2\left(\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9}+...+\frac{1}{97}-\frac{1}{99}\right)\)
\(=2\left(\frac{1}{3}-\frac{1}{99}\right)\)
\(=2.\frac{32}{99}=\frac{64}{99}\)


Giải:
Gọi số tiền thưởng của người thứ 1, 2, 3 là a, b, c
Ta có: \(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}\) và a + b = 7,2 ( triệu đồng)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b}{3+5}=\dfrac{7,2}{8}=0,9\)
\(\Rightarrow\left\{{}\begin{matrix}a=2,7\\b=4,5\\c=6,3\end{matrix}\right.\)
Vậy người 1 có số tiền thưởng là 2,7 triệu đồng
người 2 có số tiền thưởng là 4,5 triệu đồng
người thứ 3 có số tiền thưởng là 6,3 triệu đồng
Gọi số tiền thưởngcủa ba công nhân 1, 2, 3 lần lượt là a, b, c.
Theo đề bài, ta có : \(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}\)và a + b = 7,2 (triệu đồng)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b}{3+5}=\dfrac{7,2}{8}=0,9\)
Từ \(\dfrac{a}{3}=0,9\Rightarrow a=0,9\times3=2,7\)
\(\dfrac{b}{5}=0,9\Rightarrow b=0,9\times5=4,5\)
\(\dfrac{c}{7}=0,9\Rightarrow c=0,9\times7=6,3\)
Vậy số tiền được thưởng của người thứ nhất là 2,7 triệu đồng, số tiền được thưởng của người thứ hai là 4,5 triệu đồng, số tiền được thưởng của người thứ ba là 6,3 triệu đồng.
Tổng số tiền được thưởng của cả ba người là : 2,7 + 4,5 + 6, 3 = 13,5 triệu đồng.

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
BD=CE
\(\widehat{ABD}=\widehat{ACE}\)
Do đó: ΔABD=ΔACE
Suy ra: AB=AC
hay ΔABC cân tại A
b: XétΔABC có
AD là đường cao
CH là đường cao
AD cắt CH tại D
Do đó: D là trực tâm của ΔABC
=>BD vuông góc với AC

Bài 3 :
A B S M C P N x y 1 2 z 1 2
a) Kéo dài tia NM và NM cắt BC tại S
Khi đó ta có :
\(\hept{\begin{cases}\widehat{ABC}=\widehat{BSM}\left(\text{ 2 góc so le trong }\right)\\\widehat{MNP}=\widehat{BSM}\left(\text{ 2 góc so le trong }\right)\end{cases}}\Rightarrow\widehat{ABC}=\widehat{MNP}\Rightarrow\widehat{MNP}=40^o\)
b) Vẽ \(\hept{\begin{cases}\text{Bx là tia phân giác của }\widehat{ABC}\\\text{Ny là tia phân giác của }\widehat{MNP}\end{cases}}\)
\(\Rightarrow\widehat{B_1}=B_2=\widehat{N_1}=\widehat{N_2}=\frac{\widehat{ABC}}{2}=\frac{\widehat{MNP}}{2}=\frac{40^o}{2}=20^o\left(\text{do }\widehat{ABC}=\widehat{MNP}\right)\)
Vẽ Sz // Bx => \(\widehat{B_2}=\widehat{S_1}\)
Lại có \(\widehat{BSN}=\widehat{MSP}\Rightarrow\frac{\widehat{BSN}}{2}=\frac{\widehat{MSP}}{2}\Rightarrow\widehat{S_2}=\widehat{N_1}\)mà \(\widehat{S_2}\text{ và }\widehat{N_1}\)là 2 góc so le trong
=> Sz // Ny mà Sz // Bx => Bx // Ny hay tia phân giác của 2 góc \(\widehat{ABC}\text{ và }\widehat{MNP}\)song song nhau

2.
a) +) ta co: tam giác GLO
GL = 6, LO = 8, OG = 10
=> GL < LO < GO ( 6<8<10)
=> góc O < góc G < góc L ( quan hệ giữa góc và cạnh đối diện trong tam giác LOG )
+) ta co: tam giac UVW
góc V = 40, góc U = 50
=> góc W = 180 - ( góc V + goc Ư )
= 180 - ( 50 + 40)
= 90
=> góc V < góc U < góc W
=> UW < VW < VU ( quan hệ giữa cạnh và góc trong tam giác ACB )

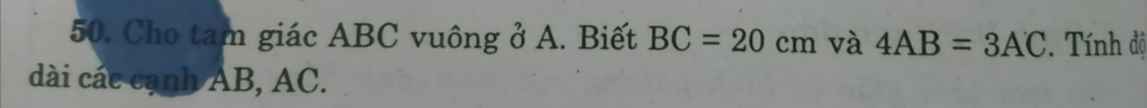

 giúp mk bài này nx nha mk cần gấp lắm r nhanh nhé các bn
giúp mk bài này nx nha mk cần gấp lắm r nhanh nhé các bn
















Đặt AB=x; AC=y
Theo đề, ta có: x/3=y/4
Đặt x/3=y/4=k
=>x=3k; y=4k
Xét ΔABC vuông tại A có \(AB^2+AC^2=BC^2\)
\(\Leftrightarrow9k^2+16k^2=20^2=400\)
=>k=4
=>AB=12cm; AC=16cm