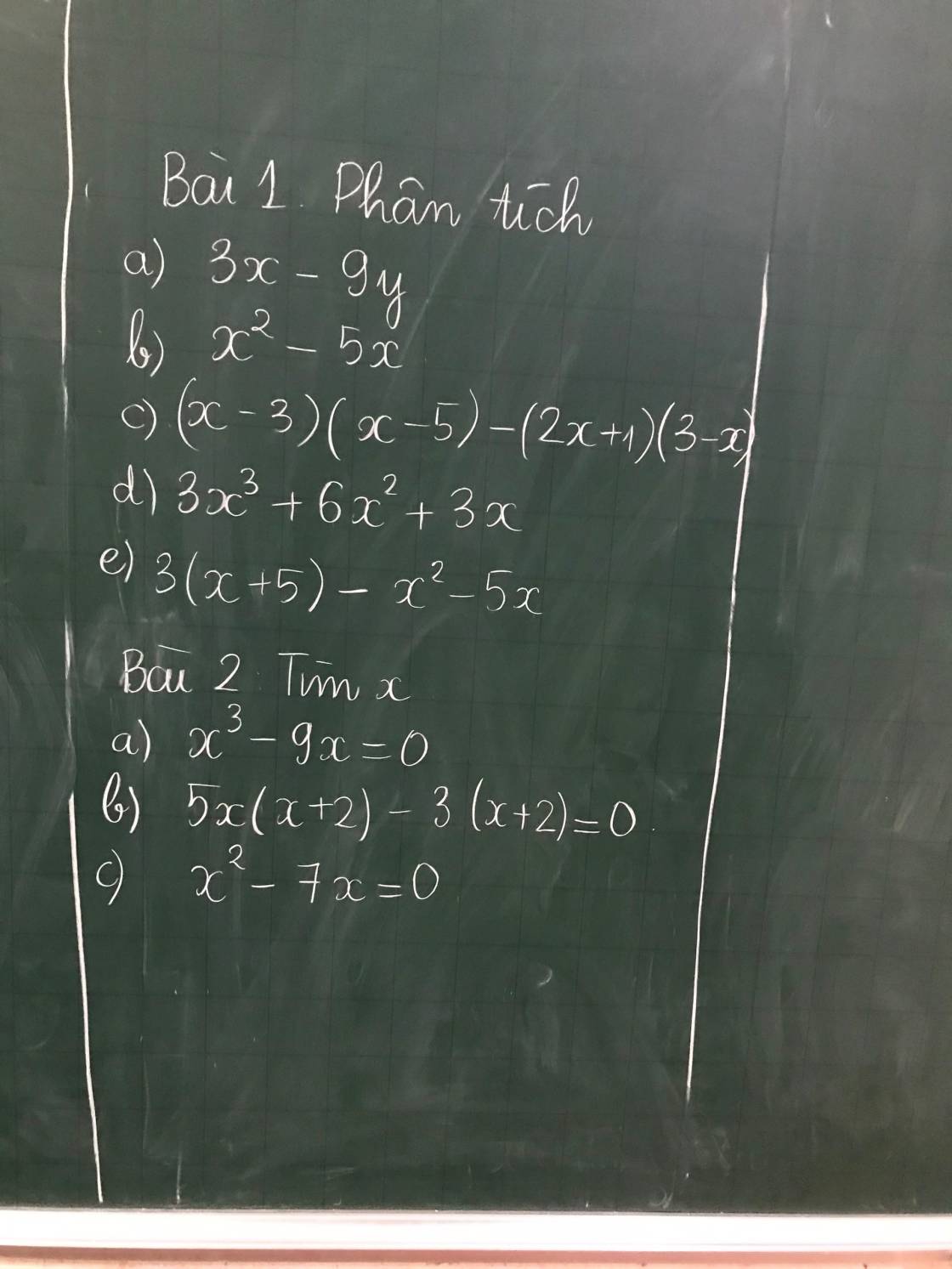NV
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 12 2016
ta co x2+3y2=4xy suy ra x2+3y2-4xy=0 suy ra x2-xy-3xy+3y2=0 suy ra x(x-y)-3y(x-y)=0 suy ra (x-3y)(x-y)=0
với x-y=0 suy ra x=y mà theo đề bài x>y>0 suy ra x-3y=0 suy ra x=3y thay vào P là xong
Ban coi co dung khong nha
Ai làm giùm cái!Làm càng nhanh càng tốt!Nhớ giải thích nha,còn đáp án thì biết rồi... (Nếu không xem được ảnh thì vào đây:https://pageshot.net/images/7221e70f-a96a-487d-baff-75847d7f7a31.png)
15 tháng 12 2016
f(1) = (3.18 - 2.16 + 15 + 2.14 - 12 +1 )5 = a0 + a1.1 + a2.12 +....+ a40.140
<=> 1024 = a0 + a1 + a2 + .... + a40
PD
2
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
11 tháng 8 2023
\(Bài.1:\\ a,3x-9y=3\left(x-3y\right)\\ b,x^2-5x=x\left(x-5\right)\\ c,\left(x-3\right)\left(x-5\right)-\left(2x+1\right)\left(3-x\right)=\left(x-3\right)\left(x-5\right)+\left(x-3\right)\left(2x+1\right)\\ =\left(x-3\right)\left(x-5+2x+1\right)=\left(x-3\right)\left(3x-4\right)\\ d,3x^3+6x^2+3x=3x\left(x^2+2x+1\right)=3x\left(x+1\right)^2\\ e,3\left(x+5\right)-x^2-5x=3\left(x+5\right)-x\left(x+5\right)\\ =\left(x+5\right)\left(3-x\right)\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
11 tháng 8 2023
\(Bài.2:\\ a,x^3-9x=0\\ \Leftrightarrow x.\left(x^2-9\right)=0\\ \Leftrightarrow x\left(x-3\right)\left(x+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x+3=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=3\end{matrix}\right.\\ b,5x\left(x+2\right)-3\left(x+2\right)=0\\ \Leftrightarrow\left(5x-3\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}5x-3=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{5}\\x=-2\end{matrix}\right.\\ c,x^2-7x=0\\ \Leftrightarrow x\left(x-7\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=7\end{matrix}\right.\)
){kind=link}
14 tháng 5 2021
c) Để A>-1 thì A+1>0
\(\Leftrightarrow\dfrac{1-x}{x+1}+1>0\)
\(\Leftrightarrow\dfrac{1-x+x+1}{x+1}>0\)
\(\Leftrightarrow\dfrac{2}{x+1}>0\)
mà 2>0
nên x+1>0
hay x>-1
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}x>-1\\x\ne1\end{matrix}\right.\)
14 tháng 5 2021
a) Ta có: \(A=\left(\dfrac{x+1}{x-1}-\dfrac{1-x}{x+1}+\dfrac{4x^2}{1-x^2}\right):\dfrac{2x^2-2}{x^2-2x+1}\)
\(=\left(\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}+\dfrac{\left(x-1\right)^2}{\left(x+1\right)\left(x-1\right)}-\dfrac{4x^2}{\left(x-1\right)\left(x+1\right)}\right):\dfrac{2\left(x^2-1\right)}{\left(x-1\right)^2}\)
\(=\dfrac{x^2+2x+1+x^2-2x+1-4x^2}{\left(x-1\right)\left(x+1\right)}:\dfrac{2\left(x-1\right)\left(x+1\right)}{\left(x-1\right)^2}\)
\(=\dfrac{-2x^2+2}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{\left(x-1\right)^2}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{-2\left(x^2-1\right)}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x-1}{2\left(x+1\right)}\)
\(=\dfrac{-2\cdot\left(x-1\right)}{2\left(x+1\right)}\)
\(=\dfrac{1-x}{x+1}\)
ML
5 tháng 8 2015
Dự đoán dấu "=" xảy ra khi x = y. Gộp một cách hợp lí các số hạng để áp dụng bất đẳng thức.
\(A=\frac{1}{x^2+y^2}+\frac{1}{2xy}+\frac{1}{2xy}\ge\frac{4}{x^2+y^2+2xy}+\frac{1}{2.\frac{\left(x+y\right)^2}{4}}=\frac{4}{\left(x+y\right)^2}+\frac{2}{\left(x+y\right)^2}=6\)
Dấu "=" xảy ra khi x = y = 1/2.
GTNN của A là 6.
\(B=\frac{1}{x^2+y^2}+\frac{1}{2xy}+\frac{1}{4xy}+4xy+\frac{8057}{4xy}\)
\(\ge\frac{4}{x^2+y^2+2xy}+2\sqrt{\frac{1}{4xy}.4xy}+\frac{8057}{\left(x+y\right)^2}=\frac{4}{\left(x+y\right)^2}+2+\frac{8057}{\left(x+y\right)^2}=8063\)
Dấu "=" xảy ra khi x = y = 1/2.
Vậy GTNN của B là 8063.