Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng

Mình thấy có phân biệt gì giữa hàm đa thức và phân thức đâu bạn.
Theo định nghĩa thì hàm đạt cực trị tại y'=0; đồng biến khi y' > 0 và nghịch biến khi y' < 0.
Cách làm bài hàm bậc 3 ở trên là chưa chính xác.

Chọn D
Ta có: y ' = 3 x 2 - 4 x , y ' ' = 6 x - 4 ;
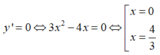
y''(0) = -4 < 0; y''(4/3) = 4 > 0. Do đó hàm số có hai cực trị là x = 0 và x = 4/3
Các mệnh đề (1); (2) và (3) sai;mệnh đề (4) đúng.

Không có khái niệm hàm số đơn điệu tại 1 điểm x hoặc y nào đó, nên bạn xem lại đề

Chọn B
![]()
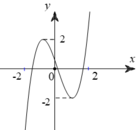
+ Đồ thị hàm số có điểm cực trị là gốc tọa độ, ta có
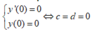
+ Đồ thị hàm số có điểm cực trị là A ( - 1 ; - 1 ) , ta có
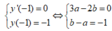
⇔ a = - 2 b = - 3
Vậy hàm số là: y = - 2 x 3 - 3 x 2

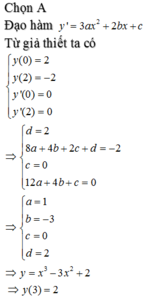

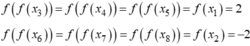
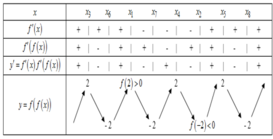
\(y'=3ax^2+2bx+c\)
Hàm có 2 điểm cực trị trái dấu khi \(y'=0\) có 2 nghiệm pb trái dấu
\(\Leftrightarrow3a.c< 0\Leftrightarrow ac< 0\)
Là a và c của hàm ban đầu