Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABD vuông tại D và ΔACE vuông tại E có
góc A chung
Do đó: ΔABD đồng dạng với ΔACE
Suy ra: AB/AC=AD/AE
hay \(AB\cdot AE=AD\cdot AC\left(1\right)\)
Xét ΔAB1C có B1D là đường cao
nên \(AD\cdot AC=AB_1^2\left(2\right)\)
Xét ΔAC1B có C1E là đường cao
nên \(AC_1^2=AE\cdot AB\left(3\right)\)
Từ (2), (1) và (3) suy ra AB1=AC1
hay ΔAB1C1 cân tại A

Đường tròn c: Đường tròn với tâm O1 và bán kính 5 Đường tròn d: Đường tròn với tâm O2 và bán kính 2 Đoạn thẳng j: Đoạn thẳng [A, B] Đoạn thẳng k: Đoạn thẳng [C, D] Đoạn thẳng l: Đoạn thẳng [O1, A] Đoạn thẳng m: Đoạn thẳng [O2, B] Đoạn thẳng n: Đoạn thẳng [O1, C] Đoạn thẳng p: Đoạn thẳng [O2, D] Đoạn thẳng q: Đoạn thẳng [O1, O2] Đoạn thẳng s: Đoạn thẳng [O2, H] O1 = (2.46, 0.9) O1 = (2.46, 0.9) O1 = (2.46, 0.9) O2 = (14, 2.1) O2 = (14, 2.1) O2 = (14, 2.1) Điểm A: Giao điểm đường của c, g Điểm A: Giao điểm đường của c, g Điểm A: Giao điểm đường của c, g Điểm B: Giao điểm đường của d, g Điểm B: Giao điểm đường của d, g Điểm B: Giao điểm đường của d, g Điểm C: Giao điểm đường của c, i Điểm C: Giao điểm đường của c, i Điểm C: Giao điểm đường của c, i Điểm D: Giao điểm đường của d, i Điểm D: Giao điểm đường của d, i Điểm D: Giao điểm đường của d, i Điểm I: Giao điểm đường của k, q Điểm I: Giao điểm đường của k, q Điểm I: Giao điểm đường của k, q Điểm H: Giao điểm đường của r, l Điểm H: Giao điểm đường của r, l Điểm H: Giao điểm đường của r, l
Gọi giao điểm của O1O2 và CD là I.
Ta thấy rằng \(\Delta O_1CI\sim\Delta O_2DI\) theo tỉ số đồng dạng là \(k=\frac{O_1C}{O_2D}=\frac{5}{2}\)
Đặt \(ID=2x\left(cm\right)\Rightarrow IC=5x\Rightarrow CD=7x\Rightarrow AB=1,5.7x=10,5x\)
Theo Pitago ta cũng có \(O_1I=\sqrt{25x^2+25};O_2I=\sqrt{4x^2+4}\left(1\right)\)
Xét hình thang vuông ABO2O1 , kẻ O2H vuông góc với AO1 , ta tính được \(HO_1=5-2=3\left(cm\right)\)
Vậy thì \(O_1O_2^2=O_2H^2+HO_1^2\Rightarrow O_1O_2=\sqrt{110,25x^2+9}\left(2\right)\)
Từ (1) và (2) suy ra \(\sqrt{110,25x^2+9}=\sqrt{25x^2+25}+\sqrt{4x^2+4}\)
\(\Leftrightarrow\sqrt{110,25x^2+9}=5\sqrt{x^2+1}+2\sqrt{x^2+1}\)
\(\Leftrightarrow\sqrt{110,25x^2+9}=7\sqrt{x^2+1}\)
\(\Leftrightarrow110,25x^2+9=49x^2+49\)
\(\Leftrightarrow x^2=\frac{32}{49}\Rightarrow O_1O_2=7.\sqrt{\frac{32}{49}+1}=9\left(cm\right)\)
Vậy O1O2 = 9 cm.

Hướng dẫn giải:
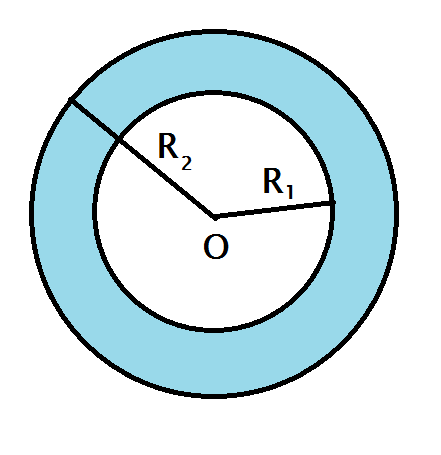
a) Diện tích hình tròn (O;R1) là S1 = πR12.
Diện tích hình tròn (O;R2) là S2 = πR22.
Diện tích hình vành khăn là:
S = S1 – S2 = πR12- πR22 = π( R12 – R22)
b) Thay số: S = 3,14. (10,52 – 7,82) = 155,1(cm2)


Bỏ chữ B đậm ở BBOC nhé!