Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(3x^2+y^2+10x-2xy+26=0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(2x^2+10x+\dfrac{5}{2}\right)+\dfrac{47}{2}=0\)
\(\Leftrightarrow\left(x-y\right)^2+2\cdot\left(x+\dfrac{5}{2}\right)^2+\dfrac{47}{2}=0\)(vô lý)
b: \(\Leftrightarrow3x^2-12x+12+6y^2-20y+\dfrac{50}{3}+\dfrac{34}{3}=0\)
\(\Leftrightarrow3\left(x-2\right)^2+6\left(y-\dfrac{5}{3}\right)^2+\dfrac{34}{3}=0\)(vô lý)
Cho tam giác ABC, 3 đường phân giác AM, BN, CP cắt nhau tại O. 3 cạnh AB, BC, CA tỉ lệ với 4,7,5
a) Tính MC, biết BC = 18cm.
b) Tính AC, biết NC - NA = 3cm
c) Tính tỉ số OP/OC
d) CM: #Hỏi cộng đồng OLM #Toán lớp 8

Cho tam giác ABC, 3 đường phân giác AM, BN, CP cắt nhau tại O. 3 cạnh AB, BC, CA tỉ lệ với 4,7,5
a) Tính MC, biết BC = 18cm.
b) Tính AC, biết NC - NA = 3cm
c) Tính tỉ số #Hỏi cộng đồng OLM #Toán lớp 8

Bài 1: Chứng minh rằng: Nếu tam giác có hai đường phân giác bằng nhau thì tam giác đó là tam giác cân.
Bài 2: Nếu
#Hỏi cộng đồng OLM
#Toán lớp 8

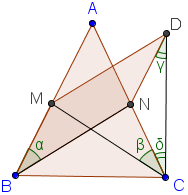
gọi 2 đường phân giác trong BN, CM bằng nhau
dựng hình bình hành BMDN và kí hiệu các góc α,β,γ,δα,β,γ,δ như hình vẽ
tam giác CMD cân tại M nên α+γ=β+δα+γ=β+δ (1)
nếu α>βα>β thì xét hai tam giác BCN và CBM có BC chung, BN=CM,CBNˆ>BCMˆ⇒CN>BMBN=CM,CBN^>BCM^⇒CN>BM
mà BM=ND⇒γ>δ⇒α+γ>β+δBM=ND⇒γ>δ⇒α+γ>β+δ, mâu thuẫn với (1)
tương tự, ko thể xảy ra trường hợp α<βα<β
suy ra α=βα=β, đpcm
Cho điểm #Hỏi cộng đồng OLM #Toán lớp 8

Auto tự vẽ hình
Giải
Kẻ \(AH\perp d,CK\perp d\)
Xét \(\Delta AHB\) và \(\Delta CKB\) là hai tam giác vuông, có:
\(\widehat{ABH}=\widehat{CBK}\) ( đối đỉnh)
AB = BC ( C đối xứng với A qua B)
=> \(\Delta AHB\) = \(\Delta CKB\) ( cạnh huyền-góc nhọn)
=> AH = CK = 2cm
Vậy B di chuyển trên d thì C di chuyển trên đường thẳng d'//d và cách d một khoảng bằng 2cm
What do you want to ask?