
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) An: "\(\forall x \in \mathbb R ,{x^2} \ge 0\)"
b) Bình: "\(\exists x \in ,{x^2} < 0\)"

Mệnh đề P đúng, bình phương của một số thực luôn lớn hơn hoặc bằng 0 (không âm).
Mệnh đề Q sai vì \({x^2} = 2 \Leftrightarrow x = \pm \sqrt 2 \notin \mathbb Q\), do đó không có số hữu tỉ nào mà bình phương của nó bằng 2.

(1) “Với mọi số tự nhiên \(x,\,\,\sqrt x \) là số vô tỉ” sai, chẳng hạn \(x = 1:\;\sqrt x = 1\) không là số vô tỉ.
(2) “Bình phương của mọi số thực đều không âm” đúng;
(3) “Có số nguyên cộng với chính nó bằng 0” đúng, số nguyên đó chính là số 0;
(4) “Có số tự nhiên n sao cho 2n – 1 = 0” sai, vì chỉ khi \(n = \frac{1}{2}\) thì 2n – 1 = 0 nhưng \(\frac{1}{2}\) không phải là số tự nhiên.

Gọi 2 số đó là a và b (a\(\ge0,b\ge0\) )
câu a
Áp dụng BĐT Bu-nhia -xkop-ki ,ta có
a+b\(\le\sqrt{\left(a^2+b^2\right)\left(1^2+1^2\right)}\)
\(\Leftrightarrow82\le\sqrt{\left(a^2+b^2\right)2}\) \(\Rightarrow\) \(6724\le\left(a^2+b^2\right)2\Leftrightarrow\left(a^2+b^2\right)\ge3362\)
Vậy Min a2+b2=3362\(\Leftrightarrow a=b=41\)

Trong tiết học môn Toán, Nam phát biểu: “Mọi số thực đều có bình phương khác 1”.
Mai phát biểu: “Có một số thực mà bình phương của nó bằng 1”
a) Phát biểu của Nam là sai. (chẳng hạn 1 và -1)
Phát biểu của Mai là đúng, số thực đó là 1 và -1.
b) Phát biểu của Nam: "\(\forall x \in \mathbb{R},\;{x^2} \ne 1\)".
Phát biểu của Mai: "\(\exists \;x \in \mathbb{R},{x^2} = 1\)".
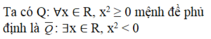
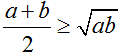
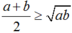
không có đáp án
Đối với mọi a thì ta luôn có \(a^2\ge0\)( Tức là ko có số nào )
Còn nếu mà cậu nghĩ / cho / tin / khẳng định số 0 là số âm thì cứ cho là " bình phương của 0 là số âm đi "