Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ý nghĩa của các con số ở trục hoành:
Các con số trên trục hoành mang ý nghĩa chỉ số trẻ em (từ 0 em đến 100 em) trong độ tuổi từ 6 đến 10 tuổi ở một vùng trên đất nước ta.
b) Tỉ lệ trẻ em từ 6 đến 10 tuổi của vùng Tây Nguyên đi học đạt 92,29% (so với dân số trong độ tuổi).
Tỉ lệ trẻ em từ 6 đến 10 tuổi của vùng đồng bằng sông Cửu Long đi học đạt 87,81% (so với dân số trong độ tuổi).
c) Đưa vào biểu đồ ta nhận thấy.
Vùng đồng bằng sông Hồng có tỉ lệ trẻ em từ 6 – 10 tuổi đi học tiểu học cao nhất và vùng đồng bằng sông Cửu Long có tỉ lệ trẻ em từ 6 – 10 tuổi đi học tiểu học thấp nhất.
a) Tỉ lệ trẻ em từ 6 đến 10 tuổi của vùng Tây Nguyên đi học đạt 92,29%.
Tỉ lệ trẻ em từ 6 đến 10 tuổi của vùng đồng bằng sông Cửu Long đi học đạt 87,81%.
b) Dựa vào biểu đồ ta nhận thấy: Vùng đồng bằng sông Hồng có tỉ lệ trẻ em từ 6 – 10 tuổi đi học tiểu học cao nhất và vùng đồng bằng sông Cửu Long có tỉ lệ trẻ em từ 6 – 10 tuổi đi học tiểu học thấp nhất.

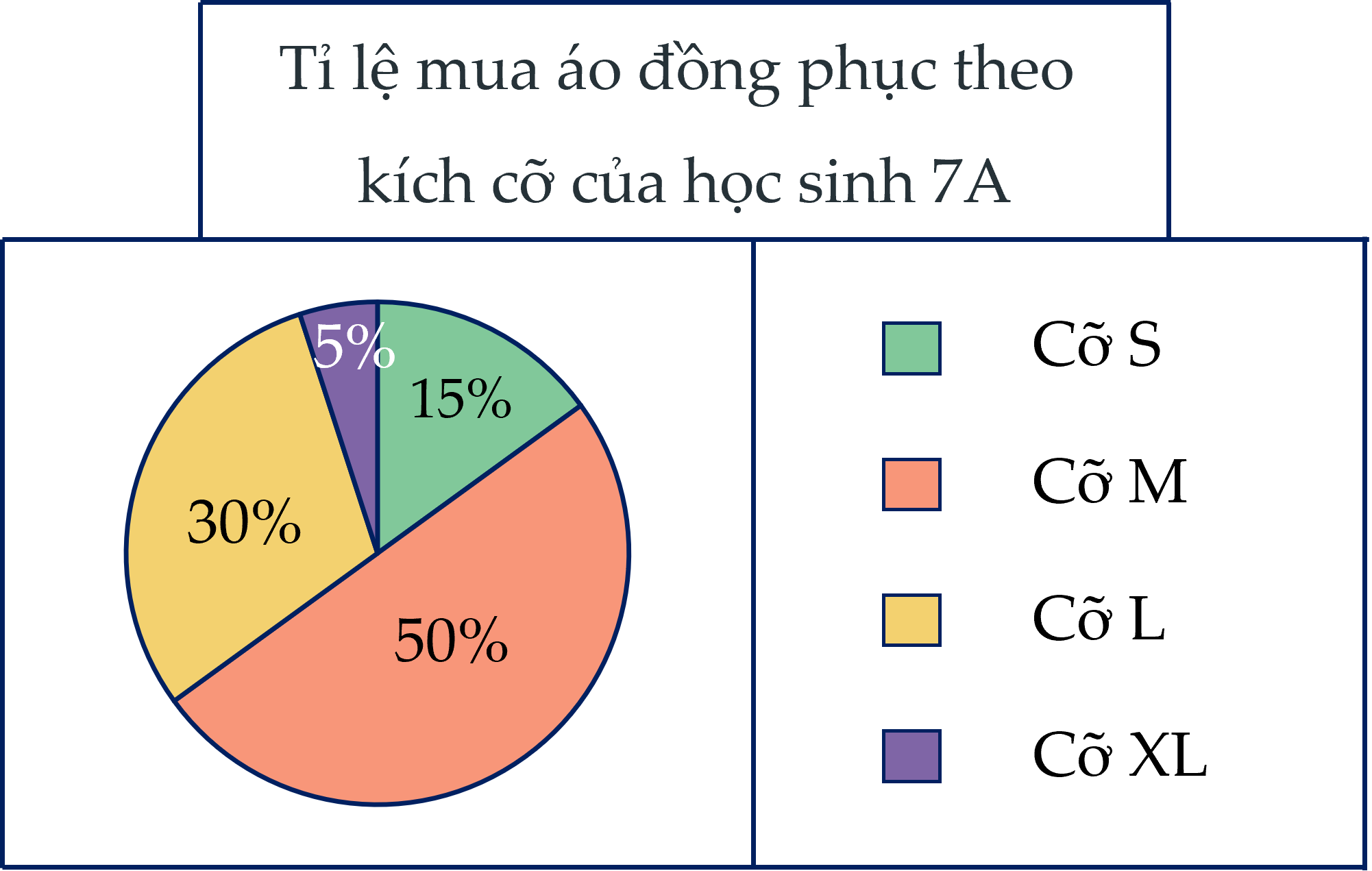
a) Cỡ áo nào có tỉ lệ học sinh đặt mua nhiều nhất? -> Cỡ M
b) Cỡ áo nào có tỉ lệ học sinh đặt mua ít nhất? -> Cỡ XL
c) Biết lớp 7A có 40 học sinh. Tính số lượng bạn đã mua áo đồng phục mỗi loại.
Số bạn mua áo cỡ S:
\(15\%.40=6\left(HS\right)\)
Số bạn mua áo cỡ M:
\(50\%.40=20\left(HS\right)\)
Số bạn mua áo cỡ L:
\(30\%.40=12\left(HS\right)\)
Số bạn mua áo cỡ XL:
\(5\%.40=2\left(HS\right)\)
Đ.số:.......

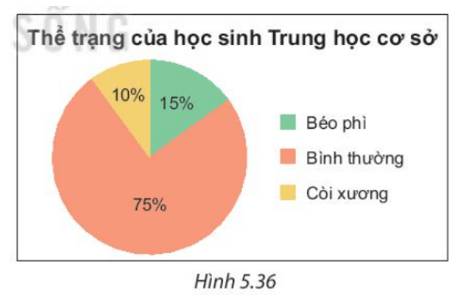
Số học sinh béo phì chiếm 15% tổng số học sinh
Số học sinh béo phì ở trường Trung học cơ sở đó là khoảng : 1500 . 15% = 225 (học sinh)

Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{6}\) đơn vị cũ.
Điểm A nằm bên phải gốc O và cách O một đoạn bằng 10 đơn vị mới. Do đó điểm A biểu diễn số hữu tỉ \(\frac{{10}}{6} = \frac{5}{3}\)
Điểm B nằm bên trái gốc O và cách O một đoạn bằng 5 đơn vị mới. Do đó điểm B biểu diễn số hữu tỉ \(\frac{{ - 5}}{6}\)
Điểm C nằm bên trái gốc O và cách O một đoạn bằng 13 đơn vị mới. Do đó điểm C biểu diễn số hữu tỉ \(\frac{{ - 13}}{6}\)

a) Dấu hiệu là diện tích rừng tập trung của tỉnh Quảng Ninh trong một số năm ,từ năm 2000 đến 2008
b)Tỉnh Quảng Ninh trong được 13,2 ha rừng
a) Dấu hiệu là diện tích rừng tập trung của tỉnh Quảng Ninh trong một số năm ,từ năm 2000 đến 2008
b)Tỉnh Quảng Ninh trong được 13,2 ha rừng
chắc là đúng

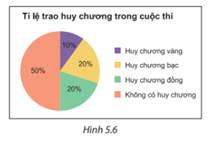
a) Huy chương bạc và huy chương đồng có cùng tỉ lệ
b) Số thí sinh không có huy chương chiếm tỉ lệ 50%. Phần quạt biểu diễn tỉ lệ này chiếm 1 nửa đường tròn.

Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:

\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

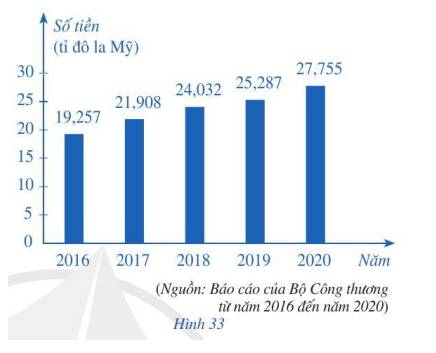
a) Tỉ số phần trăm kim ngạch xuất khẩu hàng hóa năm 2020 và kim ngạch xuất khẩu hàng hóa năm 2016 là:
\(\dfrac{{27,755}}{{19,257}}.100 = 144,129 \approx 144,13\)%
Vậy kim ngạch xuất khẩu hàng hóa năm 2020 của tỉnh Bình Dương tăng 44,13% so với năm 2016.
b) Tổng kim ngạch xuất khẩu hàng hóa của tỉnh Bình Dương trong giai đoạn từ năm 2016 đến năm 2020 là:
\(19,257 + 21,908 + 24,032 + 25,287 + 27,755 = 118,239\)(tỉ đô la Mỹ)
Vậy trong giai đoạn từ năm 2016 đến năm 2020, kim ngạch xuất khẩu hàng hóa của tỉnh Bình Dương trung bình là:
\(118,239:5 = 23,6478\)(tỉ đô la Mỹ)
c) Tỉ số giữa kim ngạch xuất khẩu hàng hóa của tỉnh Bình Dương so với kim ngạch xuất khẩu hàng hóa của cả nước năm 2016 là: \(\dfrac{{19,257}}{{176,6}} \approx 0,11\)
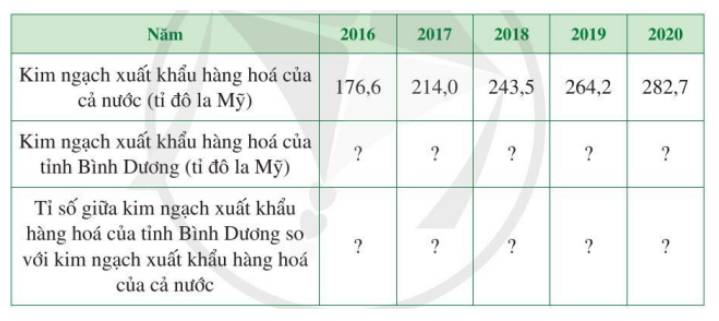
Tương tự, ta có bảng số liệu:
Năm | 2016 | 2017 | 2018 | 2019 | 2020 |
Kim ngạch xuất khẩu hàng hóa của cả nước (tỉ đô la Mỹ) | 176,6 | 214,0 | 243,5 | 264,2 | 282,7 |
Kim ngạch xuất khẩu hàng hóa của tỉnh Bình Dương (tỉ đô la Mỹ) | 19,257 | 21,908 | 24,032 | 25,287 | 27,755 |
Tỉ số giữa kim ngạch xuất khẩu hàng hóa của tỉnh Bình Dương so với kim ngạch xuất khẩu hàng hóa của cả nước | \(\dfrac{{19,257}}{{176,6}}\) \(\) | \(\dfrac{{21,908}}{{214,0}}\) | \(\dfrac{{24,032}}{{243,5}}\) | \(\dfrac{{25,287}}{{264,2}}\) | \(\dfrac{{27,755}}{{282,7}}\) |
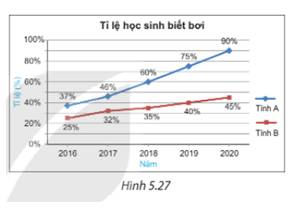





Tỉ lệ học sinh biết bơi của hai tỉnh A và B từ năm 2016 đến 2020 đều tăng.
Trong giai đoạn này, tỉnh A có tỉ lệ học sinh biết bơi tăng nhanh hơn vì độ dốc của biểu đồ đoạn thẳng của tỉnh A là lớn hơn.