Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cùng chiều : F=F1+F2=7 N.
ngược chiều :F=|F1-F2|=1 N (Hợp lực ở đây có cùng chiều với F2).
tạo với nhau 1 góc 120 độ :F2=F12+F22+2*F1*F2*cos(120) = \(\sqrt{13}\) N.
Còn nếu muốn có gia tốc thì bạn phải cho khối lượng chứ .

F=\(\sqrt{F^2_1+F_2^2+2F_1.F_2.\cos\alpha}\)\(\Rightarrow\)F2=0N

\(F_1=F.\cos30=\frac{60.\sqrt{3}}{2}=30\sqrt{3}\left(N\right)\)
\(F_2=F.\cos60=\frac{60.1}{2}=30\left(N\right)\)
Muốn thử lại xem đúng hay ko áp dụng định lý hàm sin
\(F^2=F_1^2+F_2^2+2F_1F_2.\cos\left(\widehat{F_1;F_2}\right)\)
Chắc chắn đúng =))
Tặng kèm cái hình


\(cos\alpha=\dfrac{F_1^2+F_2^2-F^2}{2.F_1.F_2}\)\(\Rightarrow\)\(\alpha\)\(\approx\)1190

Nếu F1=F2
do góc giữa vecto F1, F2=60o
áp dụng định lý hàm cos
F2=F12+ F22+2F1F2cos (vecto)
=> F1=0,58F
|
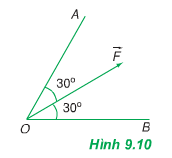
Phân tích lực F→F→ thành hai lực F1−→F1→ và F2−→F2→ theo hai phương OA và OB (hình 9.10). Giá trị nào sau đây là độ lớn của hai lực thành phần? A. F1 = F2 = F; B. F1 = F2 = 1212F; C. F1 = F2 = 1,15F; D. F1 = F2 = 0,58F. |

Ta có: \(F_1=ma_1\)
\(F_2=2F_1=ma_2\)
Có tỉ số sau : \(\frac{F_1}{F_2}=\frac{F_1}{2F_1}=\frac{ma_1}{ma_2}=\frac{1}{2}\)
=> \(\frac{a_1}{a_2}=\frac{1}{2}\)
=> \(a_2=2a_1\)

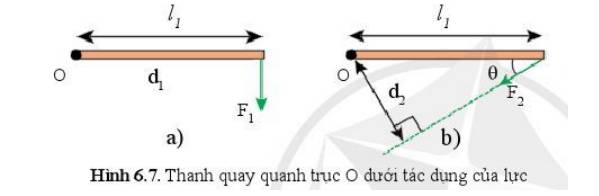
- TH1: \({F_1} > {F_2}\)
- TH2: \({F_1} < {F_2}\)