Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(W_{lkr}= \frac{W_{lk}}{A}\)
Năng lượng liên kết riêng của \(_1^2H\), \(_1^3H\), \(_2^4He\) lần lượt là 1,11 MeV; 2,83 MeV; 7,04 MeV.
Hạt nhân có năng lượng liên kết riêng càng lớn thì càng bền vững
=> Thứ tự giảm dẫn về độ bền vững là \(_2^4He\), \(_1^3H\), \(_1^2H\).

\(W_{lkr}= \frac{W_{lk}}{A}\)
Năng lượng liên kết riêng của các hạt nhân lần lượt là 1,11 MeV; 0,7075 MeV; 8,7857 MeV; 7,6 MeV.
Hạt nhân kém bền vững nhất là \(_2^4He\).

- Năng lượng liên kết của từng hạt trong phản ứng là:
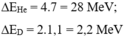
- Năng lượng tỏa ra là:
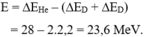

Năng lượng liên kết của từng hạt trong phản ứng là:
∆EHe = 4.7 = 28 MeV; ∆ED = 2.1,1 = 2,2 MeV
Năng lượng tỏa ra là:
E = ∆EHe – (∆ED + ∆ED) = 28 – 2.2,2 = 23,6 MeV.
Chọn đáp án B

Đáp án B
Phương pháp: Sử dụng định luật bảo toàn điện tích và số khối để viết phương trình phản ứng
Áp dụng công thức tính năng lượng tỏa ra của phản ứng hạt nhân:
![]()
Trong đó: Wlkt, Wlks lần lượt là năng lượng liên kết của các hạt trước là sau phản ứng.
Cách giải:
Năng lượng tỏa ra:
![]()
![]()
![]()
Chọn B

Năng lượng liên kết riêng của \(_3^6Li\) là \(W_{lkr1}= \frac{(3.m_p+3.m_n-m_{Li})c^2}{6}=5,2009 MeV.\ \ (1)\)
Năng lượng liên kết riêng của \(_{18}^{40}Ar\) là \(W_{lkr2}= \frac{(18.m_p+22.m_n-m_{Ar})c^2}{40}= 8,6234MeV.\ \ (2)\)
Lấy (2) trừ đi (1) => \(\Delta W = 3,422MeV.\)
Của Ar lớn hơn của Li.


bài 39, 2 hạt nhân nhẹ tổng hợp lại thành 1 hạt , A nhỏ hơn 10