Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có \(AC^2=BA^2+BC^2\)
nên ΔBAC vuông tại B
b: \(\sin BAC=\dfrac{BC}{AC}=\dfrac{42}{58}=\dfrac{21}{29}\)
\(\cos BAC=\dfrac{40}{58}=\dfrac{20}{29}\)
\(\tan BAC=\dfrac{21}{20}\)
\(\cot BAC=\dfrac{20}{21}\)
c: \(BH=\dfrac{40\cdot42}{58}=\dfrac{840}{29}\left(cm\right)\)
\(BE=\dfrac{BH^2}{BA}=\left(\dfrac{840}{29}\right)^2:40=\dfrac{17640}{841}\left(cm\right)\)

A B C D F E
a) Tam giác ABC vuông tại A (góc A = 90 độ)
Áp dụng định lý Pytago, ta có: \(AB^2+AC^2=9^2+12^2=BC^2\)
\(\Rightarrow BC=\sqrt{225}=15\) (Cm)
Áp dụng tính chất tia phân giác, ta có:
\(\frac{BD}{AB}=\frac{CD}{AC}=\frac{BD+CD}{AB+AC}=\frac{BC}{AB+AC}=\frac{15}{9+12}=\frac{5}{7}\)
\(\Rightarrow BD=\frac{5}{7}\times9=\frac{45}{7}\) (Cm)
\(CD=\frac{5}{7}\times12=\frac{60}{7}\) (Cm)

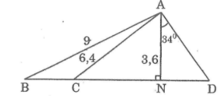
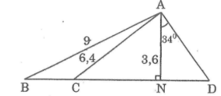
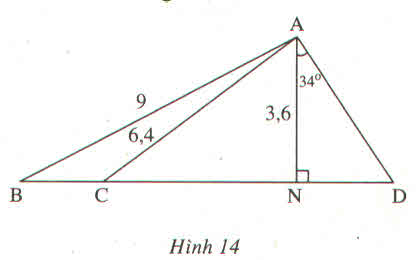
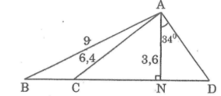
Áp dụng định lí Pi-ta-go vào tam giác vuông ANC, ta có:
A C 2 = A N 2 + N C 2 ⇒ N C 2 = A C 2 - A N 2
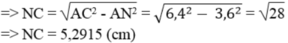

Áp dụng định lý Pitago ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{9^2+12^2}\)
\(\Rightarrow BC=15\)
Ta có:
\(sinC=\dfrac{AB}{BC}=\dfrac{9}{15}\Rightarrow sinC=\dfrac{3}{5}\)
\(\Rightarrow C\approx36^052'\)
\(B=90^0-C=53^08'\)
a) Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=9^2+12^2=225\)
hay BC=15
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{9}{15}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
\(\Leftrightarrow\widehat{B}=53^0\)