KH
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KL
MN ơi giải giúp em bài này với : a) chứng tỏ tia A3=B1 b) chứng tỏ A3 + B4= 180 độ c) chứng tỏ A1=B1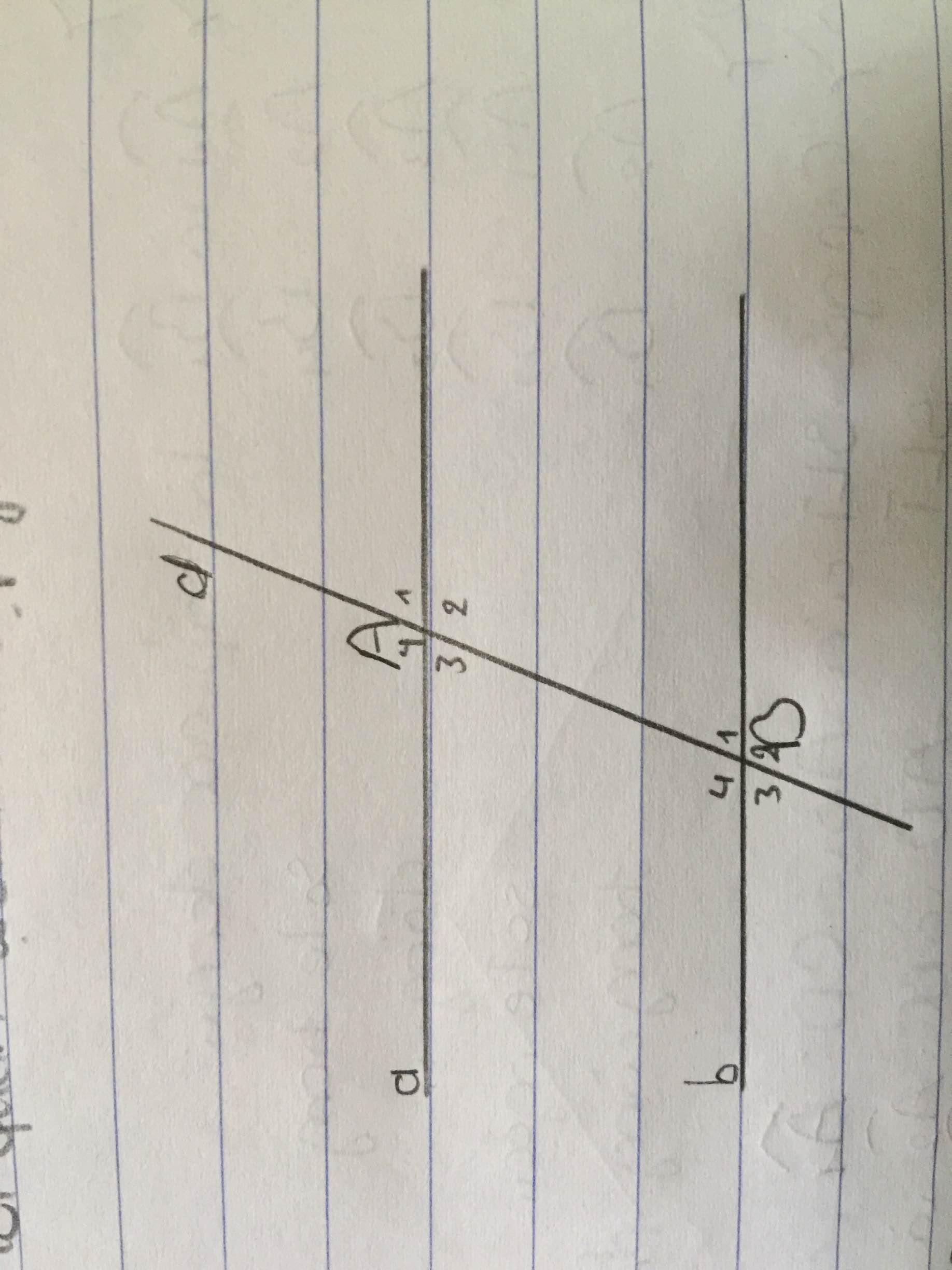
4
PN
0
H
2
KV
9 tháng 10 2023
Ta có:
∠B₂ = ∠B₁ = 70⁰ (đối đỉnh)
⇒ ∠B₂ = ∠A₁ = 70⁰
Mà ∠B₂ và ∠A₁ là hai góc đồng vị
⇒ a // b
8 tháng 11 2015
Ta có góc B=góc C=40 độ=> góc A= 180 độ- góc B- góc C= 100 độ => góc ngoài của góc A là 80 độ
Ax là phân giác của góc ngoài ở đỉnh A=> góc tạo bởi Ax và AB là 40 độ mà góc B=40 độ=> góc đó=góc B mà 2 góc ở vị trí so le trong=> Ax//BC
R
2 tháng 6 2019
Bạn có thể vẽ ra tập rồi trả lời câu hỏi mới dễ bạn à.
Còn trên đây mk ko biết vẽ hình.
Hoặc bạn có thể vào học 24 hoặc câu hỏi tương tự tham khảo.
Chúc bạn học tốt !
NN
0
20 tháng 2 2020
a) Ta có tam giác ABC cân tại A nên: \(\widehat{B}=\widehat{C}=\frac{180^0-\widehat{A}}{2}\)(1)
Xét tam giác ADE có AD=AE (gt)
=> tam giác ADE cân tại A => \(\widehat{AED}=\widehat{ADE}=\frac{180^0-\widehat{A}}{2}\)(2)
Từ (1) và (2) => \(\widehat{AED}=\widehat{B}\)
Mà 2 góc ở vị trí đồng vị nên \(DE//BC\)(đccm)
b)Ta có AB=AE+EB và AC=AD+CD mà AB=AC, AE=AD => EB= CD
Xét tam giác BEC, tam giác BCD có:
EB= CD
\(\widehat{B}=\widehat{C}\)
BC chung
=> tam giác BEC= tam giác CDB ( c_g_c)
=>\(\widehat{BEC}=\widehat{BDC}=90^0\)
=> \(CE\perp AB\)(ĐCCM)
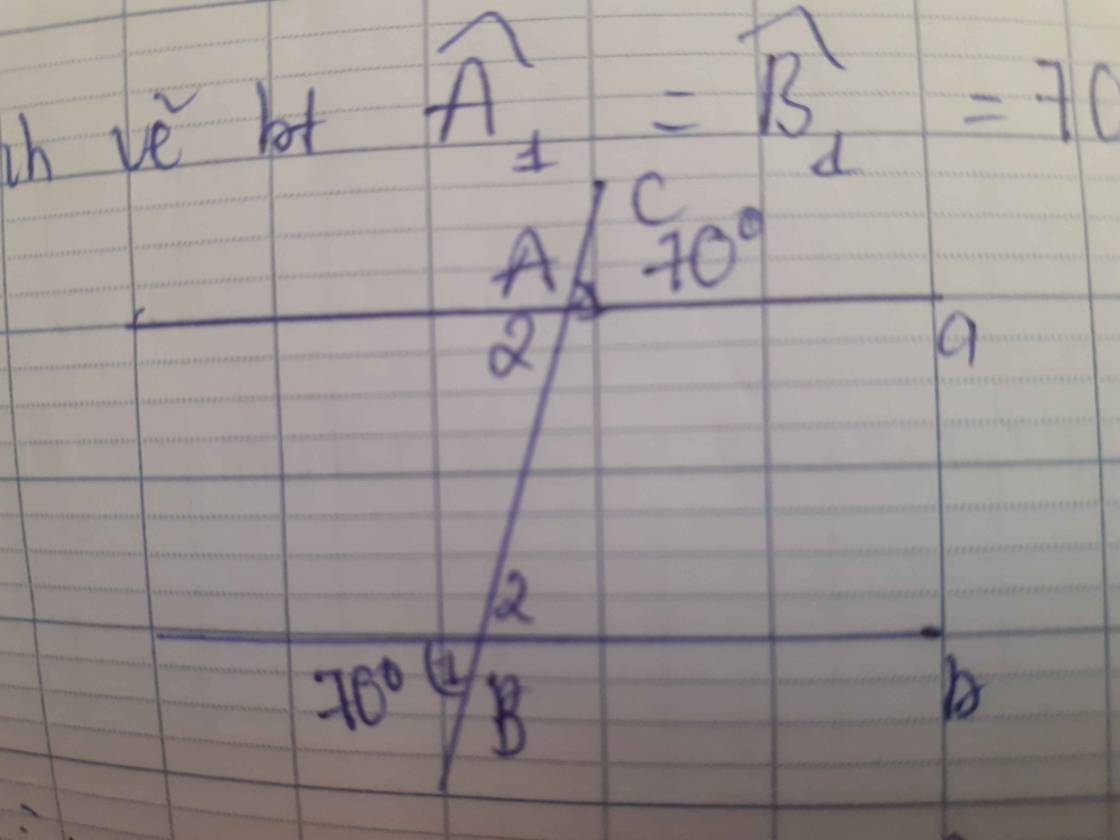
Ta có: \(\widehat{B_1}=\widehat{B_2}=50^0\)(đối đỉnh)
\(\Rightarrow\widehat{A_1}=\widehat{B_2}=50^0\)
Mà 2 góc này so le trong
=> a//b
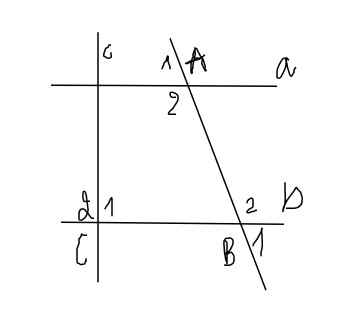
Ta có: A1 = B1 = 50 độ
Mà 2 góc này ở vị trí đồng vị
=> a//b