Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{a}{b}< \frac{a+2006}{b+2006}\)
\(\Leftrightarrow a\left(b+2006\right)< b\left(a+2006\right)\)
\(\Leftrightarrow ab+2006a< ab+2006b\)
\(\Leftrightarrow2006a< 2006b\)
\(\Leftrightarrow a< b\) (thỏa mãn đề bài)
Vậy \(\frac{a}{b}< \frac{a+2006}{b+2006}\)

1) Nếu a/b>1 thì a/b>b/b<=>a>b
2)Nếu a>b thì a.z>b.z=>a/b>z/z<=>a/b>1
3)Nếu a/b<1 thì a/b<b/b<=>a<b
4)Nếu a<b=>a.z<b.z=>a/b<z/z<=>a/b<1

Ta có:
\(\dfrac{a}{b}=\dfrac{a.d}{b.d}\) và \(\dfrac{c}{d}=\dfrac{c.b}{d.b}\)
Từ trên suy ra :
Nếu ad < bc thì \(\dfrac{a}{b}< \dfrac{c}{d}\) \(\left(ĐPCM\right)\)

Vì a < b => a + a < a + b => 2a < a + b
Do 2a < a + b nên x < z (1)
Vì a < b nên a + b < b + b => a + b < 2b
Do a + b < 2b nên z < y (2)
Từ (1) và (2) => x < z < y (đpcm)

Bài 1:
Vì \(\dfrac{a}{b}< \dfrac{c}{d}\) nên ad<bc (1)
Xét tích; a.(b+d)=ab+ad (2)
b.(a+c)=ba+bc (3)
Từ (1),(2),(3) suy ra a.(b+d)<b.(a+c) .
Do đó \(\dfrac{a}{b}< \dfrac{a+c}{b+d}\) (4)
Tương tự ta lại có \(\dfrac{a+c}{b+d}< \dfrac{c}{d}\) (5)
Kết hợp (4),(5) => \(\dfrac{a}{b}< \dfrac{a+c}{b+d}< \dfrac{c}{d}\)
hay x<y<z
Bài 2:
a) x là một số hữu tỉ \(\Leftrightarrow\)\(b-15\ne0\Leftrightarrow b\ne15\)
b)x là số hữu tỉ dương\(\Leftrightarrow b-15>0\Leftrightarrow b>15\)
c) x là số hữu tỉ âm \(\Leftrightarrow b-15< 0\Leftrightarrow b< 15\)
Bài 3:
Ta có: \(\left|x-\dfrac{1}{3}\right|\ge0\) (dấu bằng xảy ra \(\Leftrightarrow x=\dfrac{1}{3}\))
=>\(\left|x-\dfrac{1}{3}\right|+\dfrac{1}{4}\ge\dfrac{1}{4}>\dfrac{1}{5}\)
Vậy A\(>\dfrac{1}{5}\)
Bài 4:
M>0 \(\Leftrightarrow x+5;x+9\) cùng dấu.Ta thấy x+5<x+9 nên chỉ có 2 trường hợp
M>0 \(\left[{}\begin{matrix}x+5;x+9\left(duong\right)\\x+5;x+9\left(am\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x+5\ge0\\x+9\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge-5\\x\ge-9\end{matrix}\right.\)
Bài 5:
Ta dùng phương pháp phản chứng:
Giả sử tồn tại 2 số hữu tỉ x và y thỏa mãn đẳng thức \(\dfrac{1}{x+y}=\dfrac{1}{x}+\dfrac{1}{y}\)
=>\(\dfrac{1}{x+y}=\dfrac{x+y}{x.y}\Leftrightarrow\left(x+y\right)^2=x.y\)
Đẳng thức này không xảy ra vì \(\left(x+y\right)^2>0\) còn x.y <0 ( do x,y là 2 số trái dấu,không đối nhau)
Vậy không tồn tại 2 số hữu tỉ x và y trái dấu ,không đối nhau thỏa mãn đề bài

1
a) Vì \(\dfrac{a}{b}< \dfrac{c}{d}\)
\(\Rightarrow\dfrac{ad}{bd}< \dfrac{bc}{bd}\)
\(\Rightarrow ad< bc\)
2
b) Ta có : \(\dfrac{-1}{3}=\dfrac{-16}{48};\dfrac{-1}{4}=\dfrac{-12}{48}\)
Ta có dãy sau : \(\dfrac{-16}{48};\dfrac{-15}{48};\dfrac{-14}{48};\dfrac{-13}{48};\dfrac{-12}{48}\)
Vậy 3 số hữu tỉ xen giữa \(\dfrac{-1}{3}\) và \(\dfrac{-1}{4}\) là :\(\dfrac{-15}{48};\dfrac{-14}{48};\dfrac{-13}{48}\)
1a ) Ta có : \(\dfrac{a}{b}\) < \(\dfrac{c}{d}\)
\(\Leftrightarrow\) \(\dfrac{ad}{bd}\) < \(\dfrac{bc}{bd}\) \(\Rightarrow\) ad < bc
1b ) Như trên
2b) \(\dfrac{-1}{3}\) = \(\dfrac{-16}{48}\) ; \(\dfrac{-1}{4}\) = \(\dfrac{-12}{48}\)
\(\dfrac{-16}{48}\) < \(\dfrac{-15}{48}\) <\(\dfrac{-14}{48}\) < \(\dfrac{-13}{48}\) < \(\dfrac{-12}{48}\)
Vậy 3 số hữu tỉ xen giữa là.................

Bài 1:
Ta có:
\(\dfrac{a}{b}>\dfrac{c}{d}\)
\(\Leftrightarrow\dfrac{a.d}{b.d}>\dfrac{b.c}{b.d}\left(b;d>0\right)\)
\(\Leftrightarrow ad>bc\)
Vậy ...
Bài 2:
Ta có:
\(0< a< 5< b\)
\(\Leftrightarrow a;b>0\)
\(\Leftrightarrow\dfrac{b}{a}>0\)
Mà \(a< 5< b\)
\(\Leftrightarrow a< b\)
\(\Leftrightarrow\dfrac{b}{a}>1\)
Vậy ...

a: \(A=\dfrac{1.3-2.6}{2.6}-\dfrac{5}{6}:2=\dfrac{-1}{2}-\dfrac{5}{12}=\dfrac{-11}{12}\)
\(B=\left(\dfrac{47}{8}-\dfrac{9}{4}-\dfrac{1}{2}\right):\dfrac{75}{26}\)
\(=\dfrac{47-18-4}{8}\cdot\dfrac{26}{75}=\dfrac{25}{75}\cdot\dfrac{26}{8}=\dfrac{1}{3}\cdot\dfrac{13}{4}=\dfrac{13}{12}\)
b: Để A<x<B thì \(\dfrac{-11}{12}< x< \dfrac{13}{12}\)
mà x là số nguyên
nên \(x\in\left\{0;1\right\}\)
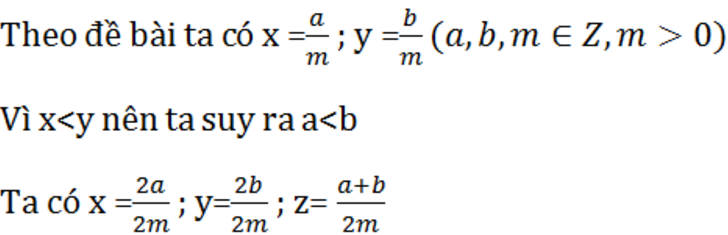
Ta có:
\(\dfrac{a}{b}=\dfrac{a\cdot\left(b+2006\right)}{b\cdot\left(b+2006\right)}=\dfrac{ab+2006a}{b^2+2006b}\\ \dfrac{a+2006}{b+2006}=\dfrac{\left(a+2006\right)\cdot b}{\left(b+2006\right)\cdot b}=\dfrac{ab+2006b}{b^2+2006b}\)
Vì \(a< b\Rightarrow2006a< 2006b\Rightarrow ab+2006a< ab+2006b\)
\(\Rightarrow\dfrac{ab+2006a}{b^2+2006b}< \dfrac{ab+2006b}{b^2+2006b}\\ \Leftrightarrow\dfrac{a}{b}< \dfrac{a+2006}{b+2006}\)