Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
ĐKXĐ: \(x>0\)
Sử dụng công thức sau: \(\log_ax=\frac{\ln x}{\ln a}\) vào bài toán ta có:
\(\log_2x+\log_3x=\log_2x\log_3x\)
\(\Leftrightarrow \frac{\ln x}{\ln 2}+\frac{\ln x}{\ln 3}=\frac{\ln x}{\ln 2}.\frac{\ln x}{\ln 3}\)
\(\Leftrightarrow \ln x\left(\frac{1}{\ln 2}+\frac{1}{\ln 3}-\frac{\ln x}{\ln 2.\ln 3}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}\ln x=0\left(1\right)\\\dfrac{1}{\ln2}+\dfrac{1}{\ln3}=\dfrac{\ln x}{\ln2.\ln3}\end{matrix}\right.\left(2\right)\)
\((1)\Leftrightarrow x=1\) (thỏa mãn)
\((2)\Leftrightarrow \frac{\ln 2+\ln 3}{\ln 2.\ln 3}=\frac{\ln x}{\ln 2.\ln 3}\)
\(\Leftrightarrow \ln x=\ln 2+\ln 3=\ln 6\Rightarrow x=6\)
Vậy \(x\in\left\{1;6\right\}\)

a)
Đặt \(\frac{x}{2}=t\Rightarrow 3^{2t}-4=5^t\)
\(\Leftrightarrow 9^t-5^t=4\)
TH1: \(t>1\Rightarrow 9^t-5^t< 4^t\)
\(\Leftrightarrow 9^t< 4^t+5^t\)
\(\Leftrightarrow 1< \left(\frac{4}{9}\right)^t+\left(\frac{5}{9}\right)^t\) \((*)\)
Ta thấy vì \(\frac{4}{9};\frac{5}{9}<1 \), do đó với \(t>1\Rightarrow \left\{\begin{matrix} \left(\frac{4}{9}\right)^t< \frac{4}{9}\\ \left(\frac{5}{9}\right)^t< \frac{5}{9}\end{matrix}\right.\)
\(\Rightarrow \left(\frac{4}{9}\right)^t+\left(\frac{5}{9}\right)^t< \frac{4}{9}+\frac{5}{9}=1\) (mâu thuẫn với (*))
TH2: \(t<1 \) tương tự TH1 ta cũng suy ra mâu thuẫn
do đó \(t=1\Rightarrow x=2\)
b)
Ta có: \(5^{2x}=3^{2x}+2.5^x+2.3^x\)
\(\Leftrightarrow (5^{2x}-2.5^{x}+1)=3^{2x}+2.3^x+1\)
\(\Leftrightarrow (5^x-1)^2=(3^x+1)^2\)
\(\Leftrightarrow (5^x-3^x-2)(5^x+3^x)=0\)
Dễ thấy \(5^x+3^x>0\forall x\in\mathbb{R}\Rightarrow 5^x-3^x-2=0\)
\(\Leftrightarrow 5^x-3^x=2\)
\(\Leftrightarrow 5^x=3^x+2\)
Đến đây ta đưa về dạng giống hệt phần a, ta thu được nghiệm \(x=1\)
c)
\((2-\sqrt{3})^x+(2+\sqrt{3})^x=4^x\)
\(\Leftrightarrow \left(\frac{2-\sqrt{3}}{4}\right)^x+\left(\frac{2+\sqrt{3}}{4}\right)^x=1\)
TH1: \(x>1\)
Vì \(\frac{2+\sqrt{3}}{4};\frac{2-\sqrt{3}}{4}<1;x> 1 \Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x< \frac{2-\sqrt{3}}{4};\left ( \frac{2+\sqrt{3}}{4} \right )^x< \frac{2+\sqrt{3}}{4}\)
\(\Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x+\left ( \frac{2+\sqrt{3}}{4} \right )^x<\frac{2-\sqrt{3}}{4}+\frac{2+\sqrt{3}}{4}=1\) (vô lý)
TH2: \(x<1 \)
\(\frac{2+\sqrt{3}}{4};\frac{2-\sqrt{3}}{4}<1; x< 1 \Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x> \frac{2-\sqrt{3}}{4};\left ( \frac{2+\sqrt{3}}{4} \right )^x> \frac{2+\sqrt{3}}{4}\)
\(\Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x+\left ( \frac{2+\sqrt{3}}{4} \right )^x>\frac{2-\sqrt{3}}{4}+\frac{2+\sqrt{3}}{4}=1\) (vô lý)
Do đó \(x=1\)

1/Lấy logarit cơ số tự nhiên 2 vế:
\(ln\left(4^{3^x}\right)< ln\left(3^{4^x}\right)\Leftrightarrow3^x.ln4< 4^x.ln3\Leftrightarrow\left(\dfrac{3}{4}\right)^x< \dfrac{ln3}{ln4}=log_43\)
\(\Rightarrow x>log_{\dfrac{3}{4}}\left(log_43\right)\)
2/ Đề là thế này hả bạn? Đột nhiên con \(x^3\) chui vào trong ngoặc đứng 1 mình làm ko hiểu gì hết \(\sqrt{log_x\left(x^3+1\right).log_{x+1}\left(x+2\right)}\)
Đầu tiên là điều kiện để logarit xác định: \(x>0\)
Ta tìm điều kiện để căn thức xác định: \(log_x\left(x^3+1\right).log_{x+1}\left(x+2\right)\ge0\)
Do \(x>0\Rightarrow\left\{{}\begin{matrix}x+1>1\\x+2>2\end{matrix}\right.\) \(\Rightarrow log_{x+1}\left(x+2\right)>0\)
\(\Rightarrow log_x\left(x^3+1\right)\ge0\Rightarrow\dfrac{ln\left(x^3+1\right)}{lnx}\ge0\)
Lại có \(x>0\Rightarrow x^3+1>1\Rightarrow ln\left(x^3+1\right)>0\)
\(\Rightarrow lnx>0\Rightarrow x>1\)
Vậy TXĐ của pt là \(x>1\)

Bạn kiểm tra lại đề. Và vào hoc 24 để đăng nhé!
Làm câu cuối:
TXĐ: \(x\in\)[ 0 ; + vô cùng )
\(y'=\frac{1}{2\sqrt{x}}-1=0\Leftrightarrow2\sqrt{x}=1\Leftrightarrow x=\frac{1}{4}\left(tm\right)\)
Vẽ bảng biến thiên:
....
Từ bảng biên thiên:
Hàm số đồng biến trong khoảng ( 0 ; 1/4 )
Hàm số nghịch biên trong khoảng ( 1/4 ; + dương vô cùng)

Lời giải:
Đặt \(\log_yx=a,\log_xy=b\). Khi đó ta có:
\(\left\{\begin{matrix} a+b=\frac{10}{3}\\ ab=\log_xy.\log_yx=1\end{matrix}\right.\)
Áp dụng định lý Viete đảo thì \(a,b\) là nghiệm của PT:
\(x^2-\frac{10}{3}x+1=0\) . PT trên có hai nghiệm \(3,\frac{1}{3}\)
Giả sử \(a=\log_yx=3\) và \(b=\log_xy=\frac{1}{3}\)
\(\left\{\begin{matrix} \log_y\left(\frac{144}{y}\right)=3\\ \log_x\left(\frac{144}{x}\right)=\frac{1}{3} \end{matrix}\right.\Rightarrow \left\{\begin{matrix} x=24\sqrt{3}\\ y=2\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow \frac{x+y}{2}=13\sqrt{3}\). Đáp án D

a) Tập xác định : D = R
limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3
Bảng biến thiên:
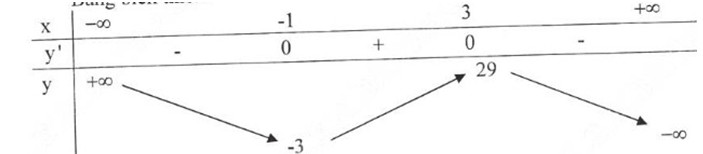
Đồ thị hàm số:
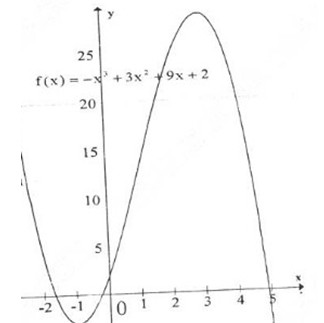
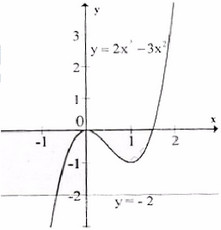
b) y=f(x) = f(x) = -x3+3x2+9x+2.
f’(x) = -3x2+6x+9. Do đó:
f’(x-1)=-3(x-1)2+6(x-1)+9
= -3x2 + 12x = -3x(x-4) > 0 ⇔ 0 < x < 4
c) f’’(x) = -6x+6
f’’(x0) = -6 ⇔ -6x0 + 6 = -6 ⇔ x0 = 2
Do đó: f’(2) = 9, f(2) = 24. Phương trình tiếp tuyến của (C) tại x0 = 2 là:
y=f’(2)(x-2) + f(2) hay y = 9x+6

Số nghiệm của các phương trình đã cho chính là số giao điểm của đồ thị hàm số y = f(x) ở vế trái của phương trình cới trục hoành ở câu a), b) và với đường thẳng y = -1 ở câu c).
a) Xét hàm số y = x3 – 3x2 + 5 . Tập xác định : R.
y' = 3x2 - 6x = 3x(x - 2); y' = 0 ⇔ x = 0,x = 2.
Bảng biến thiên:
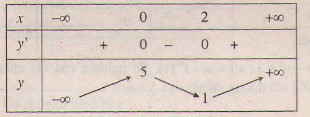
Đồ thị như hình bên.
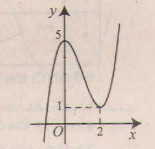
Từ đồ thị ta thấy phương trình đã cho có nghiệm duy nhất .
b) Xét hàm số y = -2x3 + 3x2 - 2 . Tập xác định : R.
y' = -6x2 + 6x = -6x(x - 1); y' = 0 ⇔ x = 0,x = 1.

Đồ thị như hình bên. Từ đồ thị ta thấy phương trình đã cho có nghiệm duy nhất .
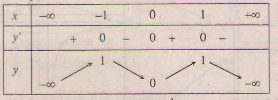
c) Xét hàm số y = f(x) = 2x2 - 2x4. Tập xác định : R.
y' = 4x - 4x3 = 4x(1 - x2); y' = 0 ⇔ x = 0,x = ±1.
Bảng biến thiên:
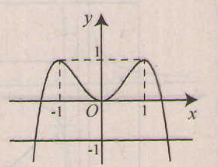
Đồ thị hàm số f(x) và đường thẳng y = -1 như hình bên.
Từ đồ thị ta thấy phương trình đã cho có hai nghiệm phân biệt.

*Đặt tên các biểu thức theo thứ tự lần lượt là A,B,C,D,E,F *
Câu 1)
Ta có: \(d(\cos x)=(\cos x)'d(x)=-\sin xdx\)
\(\Rightarrow -d(\cos x)=\sin xdx\)
\(\Rightarrow A=\int \sqrt{3\cos x+2}\sin xdx=-\int \sqrt{3\cos x+2}d(\cos x)\)
Đặt \(\sqrt{3\cos x+2}=t\Rightarrow \cos x=\frac{t^2-2}{3}\)
\(\Rightarrow A=-\int td\left(\frac{t^2-2}{3}\right)=-\int t.\frac{2}{3}tdt=-\frac{2}{3}\int t^2dt=-\frac{2}{3}.\frac{t^3}{3}+c\)
\(=-\frac{2}{9}t^3+c=\frac{-2}{9}\sqrt{(3\cos x+2)^3}+c\)
Câu 2:
\(B=\int (1+\sin^3x)\cos xdx=\int \cos xdx+\int \sin ^3xcos xdx\)
\(=\int \cos xdx+\int \sin ^3xd(\sin x)\)
\(=\sin x+\frac{\sin ^4x}{4}+c\)
Câu 3:
\(C=\int \frac{e^x}{\sqrt{e^x-5}}dx=\int \frac{d(e^x)}{\sqrt{e^x-5}}\)
Đặt \(\sqrt{e^x-5}=t\Rightarrow e^x=t^2+5\)
Khi đó: \(C=\int \frac{d(t^2+5)}{t}=\int \frac{2tdt}{t}=\int 2dt=2t+c=2\sqrt{e^x-5}+c\)

\(\Leftrightarrow3x+8-i=5+4i\)
\(\Leftrightarrow3x=-3+5i\)
\(\Leftrightarrow x=-1+\frac{5}{3}i\)
1: \(2^x=64\)
=>\(x=log_264=6\)
2: \(2^x\cdot3^x\cdot5^x=7\)
=>\(\left(2\cdot3\cdot5\right)^x=7\)
=>\(30^x=7\)
=>\(x=log_{30}7\)
3: \(4^x+2\cdot2^x-3=0\)
=>\(\left(2^x\right)^2+2\cdot2^x-3=0\)
=>\(\left(2^x\right)^2+3\cdot2^x-2^x-3=0\)
=>\(\left(2^x+3\right)\left(2^x-1\right)=0\)
=>\(2^x-1=0\)
=>\(2^x=1\)
=>x=0
4: \(9^x-4\cdot3^x+3=0\)
=>\(\left(3^x\right)^2-4\cdot3^x+3=0\)
Đặt \(a=3^x\left(a>0\right)\)
Phương trình sẽ trở thành:
\(a^2-4a+3=0\)
=>(a-1)(a-3)=0
=>\(\left[{}\begin{matrix}a-1=0\\a-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=1\left(nhận\right)\\a=3\left(nhận\right)\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}3^x=1\\3^x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=0\end{matrix}\right.\)
5: \(3^{2\left(x+1\right)}+3^{x+1}=6\)
=>\(\left[3^{x+1}\right]^2+3^{x+1}-6=0\)
=>\(\left(3^{x+1}\right)^2+3\cdot3^{x+1}-2\cdot3^{x+1}-6=0\)
=>\(3^{x+1}\left(3^{x+1}+3\right)-2\left(3^{x+1}+3\right)=0\)
=>\(\left(3^{x+1}+3\right)\left(3^{x+1}-2\right)=0\)
=>\(3^{x+1}-2=0\)
=>\(3^{x+1}=2\)
=>\(x+1=log_32\)
=>\(x=-1+log_32\)
6: \(\left(2-\sqrt{3}\right)^x+\left(2+\sqrt{3}\right)^x=2\)
=>\(\left(\dfrac{1}{2+\sqrt{3}}\right)^x+\left(2+\sqrt{3}\right)^x=2\)
=>\(\dfrac{1}{\left(2+\sqrt{3}\right)^x}+\left(2+\sqrt{3}\right)^x=2\)
Đặt \(b=\left(2+\sqrt{3}\right)^x\left(b>0\right)\)
Phương trình sẽ trở thành:
\(\dfrac{1}{b}+b=2\)
=>\(b^2+1=2b\)
=>\(b^2-2b+1=0\)
=>(b-1)2=0
=>b-1=0
=>b=1
=>\(\left(2+\sqrt{3}\right)^x=1\)
=>x=0
7: ĐKXĐ: \(x^2+3x>0\)
=>x(x+3)>0
=>\(\left[{}\begin{matrix}x>0\\x< -3\end{matrix}\right.\)
\(log_4\left(x^2+3x\right)=1\)
=>\(x^2+3x=4^1=4\)
=>\(x^2+3x-4=0\)
=>(x+4)(x-1)=0
=>\(\left[{}\begin{matrix}x+4=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\)