Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

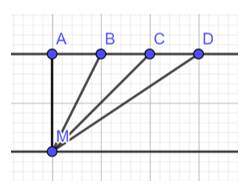
Theo hình vẽ các điểm A, B, C, D nằm trên một đường thẳng d và điểm M nằm ngoài đường thẳng đó. MA là đường vuông góc kẻ từ M đến đường thẳng d. Các đoạn thẳng MB, MC, MD là các đường xiên kẻ từ M lần lượt đến B, C và D
Ta có AB, AC, AD lần lượt là hình chiếu của MB, MC, MD xuống d. Ta có ngay AD >AC > AB suy ra
MD > MC >MB > MA
Điều đó có nghĩa là ngày hôm sau bạn Nam bơi đươci xa hơn ngày hôm trước, tức là bạn Nam tập đúng mục đích đề ra

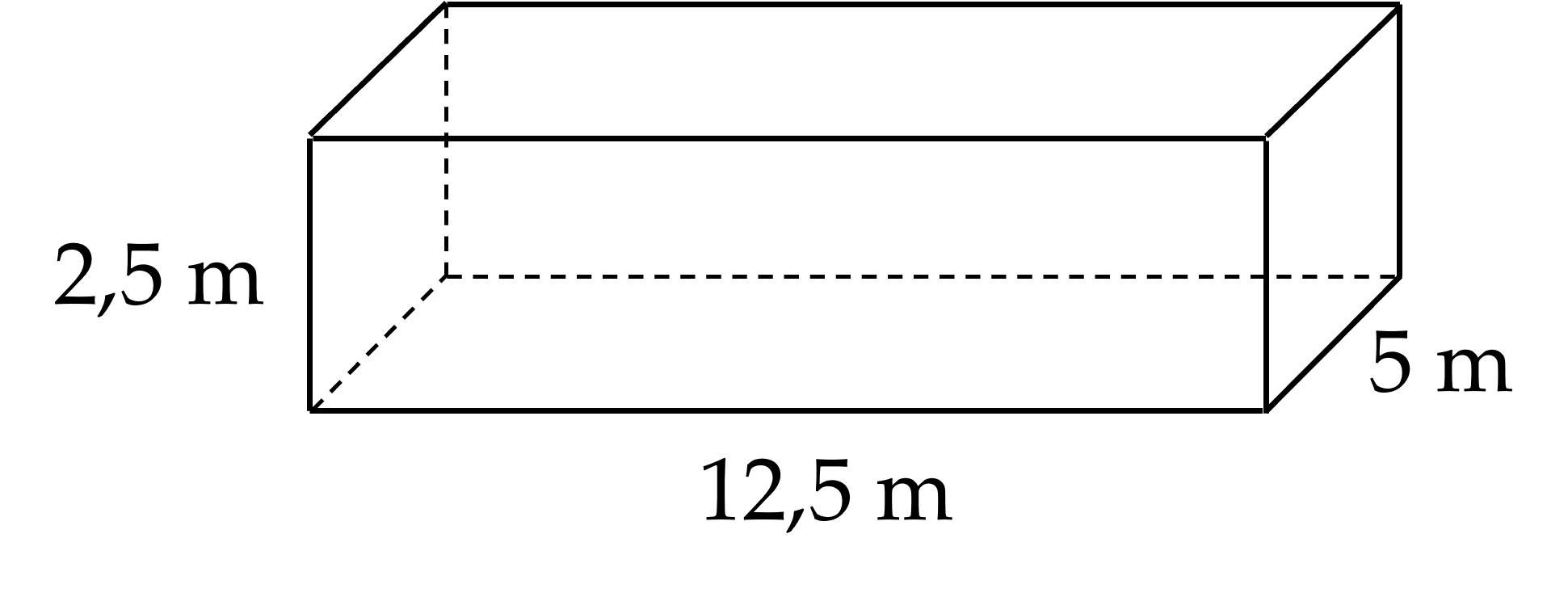
a) Thể tích hồ bơi:
12,5 . 5 . 2,5 = 156,25 (m³)
b) Diện tích đáy hồ bơi:
12,5 . 5 = 62,5 (m²)
Diện tích xung quanh hồ bơi:
(12,5 + 5) . 2 . 2,5 = 87,5 (m²)
Diện tích cần lát gạch:
87,5 + 62,5 = 150 (m²)
c) Thể tích nước trong hồ bơi:
12,5 . 5 . 1,5 = 93,75 (m³)

Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:

\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh

Do hai tam giác trên có hai cặp góc bằng nhau nên cặp góc còn lại bằng nhau.
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có:
\(\widehat A = \widehat {A'}\) (gt)
AC = A'C' (gt)
\(\widehat C = \widehat {C'}\) (cmt)
\(\Rightarrow \Delta ABC = \Delta A'B'C'\) (g.c.g)
Vậy hai tam giác đã cho bằng nhau theo trường hợp góc – cạnh – góc.

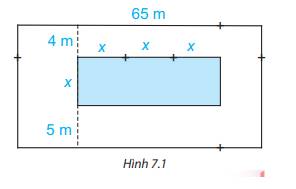
a) Bể bơi có chiều dài là 3x (m), chiều rộng là x (m) nên đa thức biểu thị diện tích bể bơi là:
\(B = 3x. x = 3x^2 (m^2)\)
b) Mảnh đất có chiều dài là 65 (m), chiều rộng là 5 + x + 4 = x + 9 (m) nên đa thức biểu thị diện tích mảnh đất là:
\(D = 65. (x+9) = 65x + 585 (m^2)\)
c) Diện tích phần đất xung quanh bể bơi = diện tích mảnh đất – diện tích bể bơi nên đa thức biểu thị diện tích phần đất xung quanh bể bơi là:
\(Q = D – B = 65x + 585 - 3x^2 = -3x^2+65x + 585(m^2)\)

Câu 10 .
a)\(P\left(x\right)=2x^2+1\)Mình làm tắt lun vì bài này dễ
b) \(P\left(\pm1\right)=2.\left(\pm1\right)^2+1=3\)Do x^2 nên 1 vs -1 k có khác nhau nên mh thay 1 lần luôn
Câu 11:
\(M+N=2x^2-2xy-3y^2+1+x^2-2xy+3y^2-1\)
\(=3x^2-4xy=x\left(2x-4y\right)\)
\(M-N=2x^2-2xy-3y^2+1-x^2+2xy-3y^2+1\)
\(=x^2-6y^2+2\)
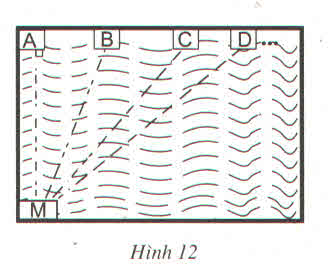



- Ta gọi thành hồ bơi đối diện là đường thẳng AD
- Bạn Minh bơi đường ngắn nhất khi bơi từ điểm M 1 đường vuông góc với AD do đoạn thẳng nối từ 1 điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên .
- Ta thấy AM vuông góc AD nên AM là đường ngắn nhất