
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: \(\dfrac{2x^3+3x^2-2x-1}{2x+3}\)
\(=\dfrac{2x^3+3x^2-2x-3+2}{2x+3}\)
\(=\dfrac{x^2\left(2x+3\right)-\left(2x+3\right)+2}{2x+3}\)
\(=x^2-1+\dfrac{2}{2x+3}\)
vậy: \(2x^3+3x^2-2x-1=\left(x^2-1\right)\left(2x+3\right)+2\)
c: \(3x\left(x-2\right)+5\left(2-x\right)=0\)
=>3x(x-2)-5(x-2)=0
=>(x-2)(3x-5)=0
=>\(\left[{}\begin{matrix}x-2=0\\3x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{5}{3}\end{matrix}\right.\)


1.
a) Hai đại lượng x, y tỉ lệ thuận với nhau
b)Hai đại lượng x, y không tỉ lệ thuận với nhau

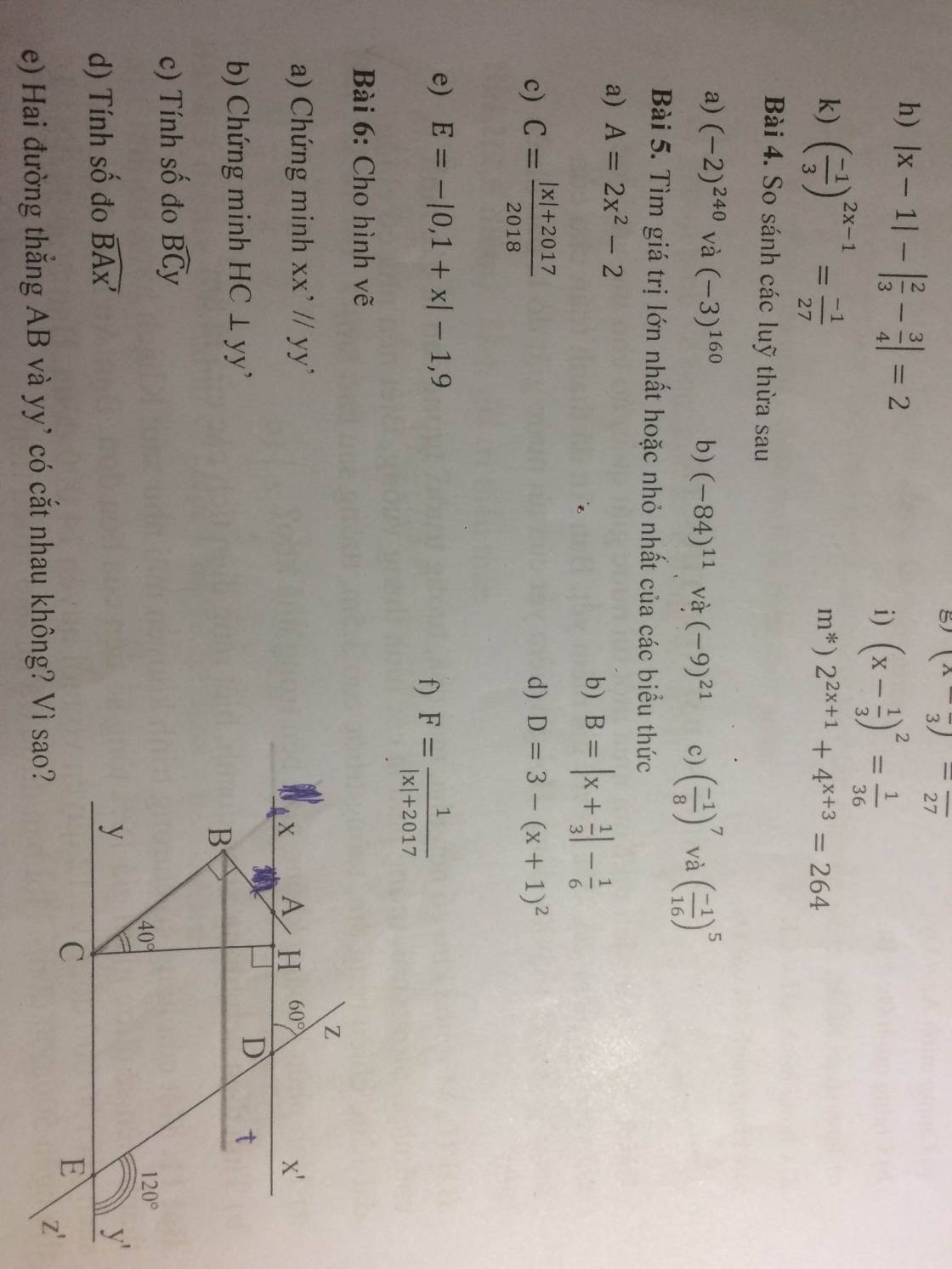
a) ∠CEz + ∠zEy' = 180⁰ (kề bù)
⇒ ∠CEz = 180⁰ - ∠zEy'
= 180⁰ - 120⁰
= 60⁰
⇒ ∠CEz = ∠xDz = 60⁰
Mà ∠CEz và ∠xDz là hai góc đồng vị
⇒ xx' // yy'
b) Do HC ⊥ xx' (gt)
xx' // yy' (cmt)
⇒ HC ⊥ yy'
c) Do HC ⊥ yy' (cmt)
⇒ ∠HCy = 90⁰
⇒ ∠BCy = ∠HCy - ∠BCH
= 90⁰ - 40⁰
= 50⁰
c) Vẽ tia Bt // xx'//yy'
⇒ ∠CBt = ∠BCy = 50⁰ (so le trong)
⇒ ∠ABt = ∠ABC - ∠CBt
= 90⁰ - 50⁰
= 40⁰
Do Bt // xx'
⇒ ∠xAB = ∠ABt = 40⁰ (so le trong)
Ta có:
∠BAx' + ∠xAB = 180⁰ (kề bù)
⇒ ∠BAx' = 180⁰ - ∠xAB
= 180⁰ - 40⁰
= 140⁰
e) Do AB cắt tia Bt tại B
Mà Bt // yy'
⇒ AB cắt yy'

Câu 15:
Gọi số tiền lớp 7A,7B,7C đóng góp đc lần lượt là a,b,c
Theo đề, ta có: a/5=b/6=c/7 và a+b+c=2700000
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{5}=\dfrac{b}{6}=\dfrac{c}{7}=\dfrac{a+b+c}{5+6+7}=\dfrac{2700000}{18}=150000\)
=>a=750000; b=900000; c=1050000

Bài 1:
a: \(\dfrac{2x^3+3x^2-2x-1}{2x+3}\)
\(=\dfrac{2x^3+3x^2-2x-3+2}{2x+3}\)
\(=\dfrac{x^2\left(2x+3\right)-\left(2x+3\right)+2}{2x+3}\)
\(=x^2-1+\dfrac{2}{2x+3}\)
vậy: \(2x^3+3x^2-2x-1=\left(x^2-1\right)\left(2x+3\right)+2\)
b: \(3x\left(x-2\right)+5\left(2-x\right)=0\)
=>3x(x-2)-5(x-2)=0
=>(x-2)(3x-5)=0
=>\(\left[{}\begin{matrix}x-2=0\\3x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{5}{3}\end{matrix}\right.\)
Bài 2:
\(A=\left(\dfrac{2xy}{x^2-y^2}+\dfrac{x-y}{2x+2y}\right)\cdot\dfrac{2x}{x+y}+\dfrac{y}{x-y}\)
\(=\left(\dfrac{2xy}{\left(x-y\right)\left(x+y\right)}+\dfrac{x-y}{2\left(x+y\right)}\right)\cdot\dfrac{2x}{x+y}+\dfrac{y}{x-y}\)
\(=\dfrac{4xy+\left(x-y\right)^2}{2\left(x+y\right)\left(x-y\right)}\cdot\dfrac{2x}{x+y}+\dfrac{y}{x-y}\)
\(=\dfrac{\left(x+y\right)^2\cdot2x}{2\left(x+y\right)^2\cdot\left(x-y\right)}+\dfrac{y}{x-y}\)
\(=\dfrac{x}{x-y}+\dfrac{y}{x-y}=\dfrac{x+y}{x-y}\)
b: \(\dfrac{x^2+y^2}{xy}=\dfrac{25}{12}\)
=>\(12\left(x^2+y^2\right)-25xy=0\)
=>\(12x^2-16xy-9xy+12y^2=0\)
=>\(4x\left(3x-4y\right)-3y\left(3x-4y\right)=0\)
=>\(\left(3x-4y\right)\left(4x-3y\right)=0\)
=>\(\left[{}\begin{matrix}3x-4y=0\\4x-3y=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}y\\x=\dfrac{3}{4}y\end{matrix}\right.\)
x<y<0 nên \(x=\dfrac{4}{3}y\)
\(A=\dfrac{x+y}{x-y}=\dfrac{\dfrac{4}{3}y+y}{\dfrac{4}{3}y-y}=\dfrac{7}{3}:\dfrac{1}{3}=7\)