Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài này làm sao vậy khó quá bạn vào giúp mình giải với mình k xem đc trả lời của bài này

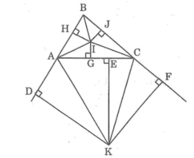
Kẻ IH ⊥ AB, IJ ⊥ BC, IG ⊥ AC, KD ⊥ AB, KE ⊥ AC, KF ⊥ BC
Vì I nằm trên tia phân giác của ∠(BAC) nên IH = IG (tính chất tia phân giác)
Vì I nằm trên tia phân giác của ∠(BCA) nên IJ = IG (tính chất tia phân giác)
Suy ra: IH = IJ
Do đó I nằm trên tia phân giác của ∠(ABC) (1)
Vì K nằm trên tia phân giác của ∠(DAC) nên KD = KE (tính chất tia phân giác)
Vì K nằm trên tia phân giác của ∠(ACF) nên KE = KF (tính chất tia phân giác)
Suy ra: KD = KF
Do đó K nằm trên tia phân giác của ∠(ABC) (2)
Từ (1) và (2) suy ra: B, I, K thẳng hàng.

A B C K I
Các đường phân giác của các góc ngoài tại đỉnh A và C của \(\Delta ABC\) cắt nhau tại K nên BK là tia phân giác của góc B.
Các tia phân giác các góc A và C của \(\Delta ABC\) cắt nhau tại I nên BI là tia phân giác của góc B. Do đó ba điểm B, I, K thẳng hàng.

Kẻ IH ⊥ AB, IJ ⊥ BC, IG ⊥ AC, KD ⊥ AB, KE ⊥ AC, KF ⊥ BC
Vì I nằm trên tia phân giác của ∠(BAC) nên IH = IG (tính chất tia phân giác)
Vì I nằm trên tia phân giác của ∠(BCA) nên IH = IG (tính chất tia phân giác)
Suy ra: IH = IJ
Do đó I nằm trên tia phân giác của (ABC) (1)
Vì K nằm trên tia phân giác của ∠(DAC) nên KD = KE (tính chất tia phân giác)
Vì K nằm trên tia phân giác của ∠(ACF) nên KE = KF (tính chất tia phân giác)
Suy ra: KD = KF
Do đó K nằm trên tia phân giác của ∠(ABC) (2)
Từ (1) và (2) suy ra: B, I, K thẳng hàng.

Lời giải:
Kẻ $KM, KT, KN$ lần lượt vuông góc với $AB, AC, BC$.
Vì $K$ thuộc tia phân giác $\widehat{MAC}$ nên $KM=KT$ (tính chất quen thuộc)
Vì $K$ thuộc tia phân giác $\widheat{ACN}$ nên $KN=KT$
$\Rightarrow KM=KN$
$\Rightarrow K$ thuộc tia phân giác $\widehat{MBN}$ hay $\widehat{ABC}$
Do đó $BI, BK$ cùng là tia phân giác $\widehat{ABC}$
$\Rightarrow B,I,K$ thẳng hàng

Cái này bạn đổi điểm K thành điểm M là xong nha
Kẻ IG,IK,IH lần lượt vuông góc với AB,BC,AC
Kẻ MO,MD,ME lần lượt vuông góc với AB,BC,AC
Xét ΔBKI vuông tại K và ΔBGI vuông tại G có
BI chung
góc KBI=góc GBI
Do đó: ΔBKI=ΔBGI
Suy ra: IK=IG(1)
Xét ΔCKI vuông tại K và ΔCHI vuông tại H có
CI chung
góc KCI=góc HCI
Do dó: ΔCKI=ΔCHI
Suy ra: IK=IH(2)
Từ (1) và (2) suy ra IG=IH
mà I nằm trong ΔABC và IG,IH là các đường cao ứng với các cạnh AB,AC
nên AI là phân giác của góc BAC(3)
Xét ΔBOM vuông tại O và ΔBDM vuông tại D có
BM chung
góc OBM=góc DBM
Do đó: ΔBOM=ΔBDM
Suy ra: MO=MD(4)
Xét ΔMDC vuông tại D và ΔMEC vuông tại E có
CM chung
góc DCM=góc ECM
Do đó: ΔMDC=ΔMEC
Suy ra: MD=ME(5)
Từ (4) và (5) suy ra MO=ME
mà M nằm ngoài ΔABC và MO,ME là các đường cao ứng với các cạnh AB,AC
nên AM là phân giác của góc BAC(6)
Từ (3) và (6) suy ra A,I,M thẳng hàng
Hai phân giác trong của hai \(\widehat{B}\) và \(\widehat{C}\)cắt nhau tại I nên I phải thuộc phân giác \(\widehat{A}\).
Từ D hạ DH, DK, DJ vuông góc lần lượt với AB, BC, AC
Ta có: DH = DK (do D thuộc phân giác ngoài của \(\widehat{B}\))
Tương tự: DK = DJ => DH = DJ
=> D thuộc phân giác góc A hay D thuộc AD. Vậy A, I, D thẳng hàng.