Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải: Đề bài có vẻ thừa dữ kiện.
Theo tính chất tia phân giác:
a)
$\frac{S_{ADB}}{S_{ADC}}=\frac{BD}{DC}=\frac{6}{4,5}=\frac{4}{3}$
b)
$\frac{S_{ADB}}{S_{ADC}}=\frac{BD}{DC}=\frac{BC-DC}{DC}=\frac{7-3}{3}=\frac{4}{3}$

a:
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>\(BC=\sqrt{625}=25\left(cm\right)\)
Ta có: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot15\cdot20=150\left(cm^2\right)\)
Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{CD}=\dfrac{AB}{AC}\)
=>\(\dfrac{BD}{CD}=\dfrac{3}{4}\)
=>\(\dfrac{CD}{BD}=\dfrac{4}{3}\)
=>\(\dfrac{CD+BD}{BD}=\dfrac{4+3}{3}\)
=>\(\dfrac{BC}{BD}=\dfrac{7}{3}\)
=>\(BD=\dfrac{3}{7}BC\)
=>\(S_{ABD}=\dfrac{3}{7}\cdot S_{ABC}\)
b: Vì I là trung điểm của BC
nên \(S_{ABI}=\dfrac{1}{2}\cdot S_{ABC}\)
=>\(\dfrac{S_{ABD}}{S_{ABI}}=\dfrac{3}{7}:\dfrac{1}{2}=\dfrac{6}{7}\)
c: \(S_{ABD}=\dfrac{3}{7}\cdot S_{ABC}=\dfrac{3}{7}\cdot140=60\left(cm^2\right)\)
\(S_{ABI}=\dfrac{7}{6}\cdot S_{ABD}=\dfrac{7}{6}\cdot60=70\left(cm^2\right)\)
ta có: \(S_{ABD}+S_{AID}=S_{ABI}\)
=>\(S_{AID}+60=70\)
=>\(S_{AID}=10\left(cm^2\right)\)

a, Vì AD là phân giác nên \(\frac{AB}{AC}=\frac{DB}{DC}\Rightarrow\frac{DC}{AC}=\frac{DB}{AB}\)
Theo tc dãy tỉ số bằng nhau
\(\frac{DC}{AC}=\frac{DB}{AB}=\frac{BC}{AB+AC}=\frac{10}{15}=\frac{2}{3}\Rightarrow DC=6cm;DB=4cm\)
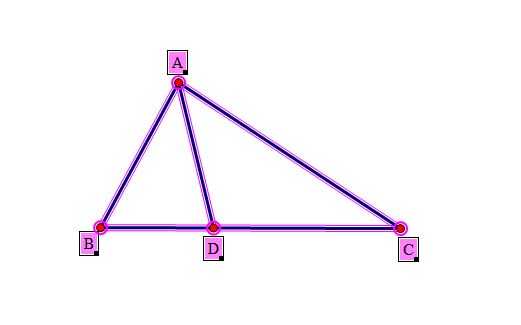
Kẻ AH⊥BC tại H
Xét ΔABD có
AH là đường cao ứng với cạnh BD(AH⊥BC, D∈BC)
nên \(S_{ABD}=\dfrac{AH\cdot BD}{2}\)
Xét ΔACD có
AH là đường cao ứng với cạnh CD(AH⊥BC, D∈BC)
nên \(S_{ACD}=\dfrac{AH\cdot CD}{2}\)
Ta có: \(\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{AH\cdot BD}{2}:\dfrac{AH\cdot CD}{2}\)
\(\Leftrightarrow\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{AH\cdot BD}{2}\cdot\dfrac{2}{AH\cdot CD}=\dfrac{BD}{CD}\)(1)
Xét ΔABC có
AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)(2)
Từ (1) và (2) suy ra \(\dfrac{S_{ADB}}{S_{ADC}}=\dfrac{AB}{AC}\)
Vậy: Tỉ số diện tích của hai tam giác này bằng tỉ số giữa hai cạnh kề hai đoạn thẳng được tạo bởi tia phân giác kẻ xuống cạnh tương ứng