Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:\(\left(x-y\right)\left(x^2+xy+y^2\right)=x^3-y^3\)
với \(x=-10;y=2\) ,ta có:
\(\left(-10\right)^3-2^3=-1000-8=-1008\)
với \(x=-1;y=0\)
\(\left(-1\right)^3-0^3=-1-0=-1\)
với \(x=2;y=-1\) ,ta có:
\(2^3-\left(-1\right)^3=8-\left(-1\right)=8+1=9\)
với \(x=-0,5;y=1,25\), ta có:
\(\left(-0,5\right)^3-1,25^3=0-2=-2\)
Ta có bảng sau;
| Giá trị của x và y |
Giá trị của biểu thức \(\left(x-y\right)\left(x^2+xy+y^2\right)\) |
| \(x=-10;y=2\) | \(\left(x-y\right)\left(x^2+xy+y^2\right)=-1008\) |
| \(x=-1;y=0\) | \(\left(x-y\right)\left(x^2+xy+y^2\right)=-1\) |
| \(x=2;y=-1\) | \(\left(x-y\right)\left(x^2+xy+y^2\right)=9\) |
| \(x=-0,5;y=1,25\) | \(\left(x-y\right)\left(x^2+xy+y^2\right)=-2\) |
Trước hết, ta làm tính nhân để rút gọn biểu thức, ta được:
(x - y)(x2 + xy + y2) = x . x2 + x . xy + x . y2 + (-y) . x2 + (-y) . xy + (-y) . y2
= x3 + x2y + xy2 – yx2 – xy2 – y3 = x3 – y3
Sau đó tính giá trị của biểu thức x3 – y3
Ta có:
Khi x = -10; y = 2 thì A = (-10)3 – 23 = -1000 – 8 = 1008
Khi x = -1; y = 0 thì A = (-1)3 – 03 = -1
Khi x = 2; y = -1 thì A = 23 – (-1)3 = 8 + 1 = 9
Khi x = -0,5; y = 1,15 thì
A = (-0,5)3 – 1,253 = -0,125 – 1.953125 = -2,078125

a) Ta có :
\(5x-3=x^2-3x+12\left(1\right)\)
\(x^2-3x+12=\left(x+1\right)\left(x-3\right)\left(2\right)\)
\(\left(x+1\right)\left(x-3\right)=5x-3\left(3\right)\)
b) Lập bảng :
| x | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| 5x - 3 | -28 | -23 | -18 | -13 | -8 | -3 | 2 | 7 | 12 | 17 | 22 |
| \(x^2-3x+12\) | 52 | 40 | 30 | 22 | 16 | 12 | 10 | 10 | 12 | 16 | 22 |
| (x+1)(x-3) | 32 | 21 | 12 | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 |
Từ bảng trên , ta có :
- Phương trình (1) có có tập nghiệm là \(S=\left\{3;5\right\}\)
- Phương trình (2) vô nghiệm \(S=\varnothing\)
- Phương trình (3) có tập nghiệm là \(S=\left\{0\right\}\)

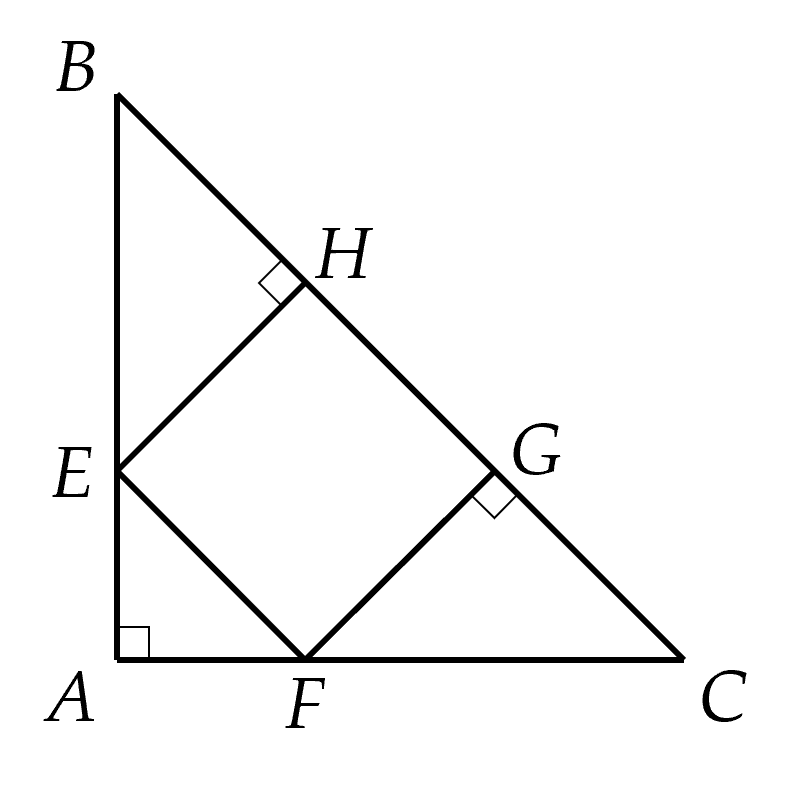
a) Δ��� Tam giác ABC vuông cân nên góc B= góc C = 45 độ
Tam giácBHE vuông tại H có góc BEH + góc B = 90 độ
Suy ra góc BEH = 90 độ - 45 độ = 45 độ nên góc B= góc BEH = 45 độ
Vậy tam giác BEH vuông tại H
b) Chứng minh tương tự như câu a ta được tam giác CFG vuông tại G nên GF=GC và HB=HE
Lại có BH=HG=GC suy ra EH=HG=GF và EH//FG ( cùng vuông góc với BC)
Tứ giác EFGH có EH//FG, EH=FG
=>tứ giác EFGH là hình bình hành
Xét hình bình hành có một góc vuông là góc H nên là hình chữ nhật
Mà hình chữ nhật có hai cạnh kề bằng nhau là EH=HG nên là hình vuông
Vậy EFGH là hình vuông
a) Δ���ΔABC vuông cân nên �^=�^=45∘.B=C=45∘.
Δ���ΔBHE vuông tại �H có ���^+�^=90∘BEH+B=90∘
Suy ra ���^=90∘−45∘=45∘BEH=90∘−45∘=45∘ nên �^=���^=45∘B=BEH=45∘.
Vậy Δ���ΔBEH vuông cân tại �.H.
b) Chứng minh tương tự câu a ta được Δ���ΔCFG vuông cân tại �G nên ��=��GF=GC và ��=��HB=HE
Mặt khác ��=��=��BH=HG=GC suy ra ��=��=��EH=HG=GF và ��EH // ��FG (cùng vuông góc với ��)BC)
Tứ giác ����EFGH có ��EH // ��,��=��FG,EH=FG nên là hình bình hành.
Hình bình hành ����EFGH có một góc vuông �^H nên là hình chữ nhật
Hình chữ nhật ����EFGH có hai cạnh kề bằng nhau ��=��EH=HG nên là hình vuông.

Thay x = -1, y = 1 vào biểu thức, ta được
a(-1)(-1 - 1) + 13(-1 + 1) = -a(-2) + 10 = 2a.
Vậy đánh dấu x vào ô trống tương ứng với 2a.

a)
Tháng | 1 | 2 | 3 | 4 |
Số tấn đã bán | 200,5 | 183,6 | 215,5 | 221,9 |
b)


Trả lời
Số tiền có trong túi là:
Nếu muốn chia 6 dư 4 thì mỗi số chia hết cho 6 ta tăng thêm 4 đơn vị.
Mà 6:6=1, ta sẽ tăng thêm 4 đơn vị vậy là 10:6=1 dư 4 nhưng lại chia hết cho 5. Nên ta sẽ tìm một số khác.
Số tiếp theo chia hết cho 6 là: 12:6=2, + thêm 4 =16:4=2 dư 4 nhưng vẫn chưa chia 5 dư 3 mà chỉ dư 1.
Và ta thấy 1 điều nếu 1 số tiếp theo chia hết cho 6 thì sẽ tăng lên 1 đơn vị dư của 5.
Nên để chia 5 dư 3 và chia 6 dư 4 thì:
(6.4)+4=28.
6 nhân 1 + 4=10 chia 5 dư 0, vậy để chia 5 dư 3 thì ta cộng thêm 3 lần số 6 nữa thì có cách làm như trên.
Vậy số cần tìm là 28.
Mà 28 chia 7 là chia hết nên dư 0 đồng !
rất vui khi đc giúp bn, mk giải thích theo cách hiểu !
Cảm ơn bạn Song tử .... Tn(siêu quậy) nhiều nha ! Vì bạn trả lời đúng ( mặc dù trên mạng cũng có đáp án rồi , hic hic . Nhưng mà vẫn nhanh tay nên mình cũng k cho 1 cái ) và còn nhanh tay nữa nên mình k cho bạn rồi nha ! Bây giờ vì đã có bạn trả lời rồi nên mình công bố kết quả từ trang nguồn VNExpress luôn nha !
Đáp án : 0 đồng .
Theo yêu cầu bài ra , ta sẽ phải tìm số tiền là số nhỏ nhất chia cho 6 dư 4 và chia cho 5 dư 3 .
Số đó chia cho 6 dư 4 nên sẽ có dạng 6 x k + 4 . Số này lại chia cho 5 dư 3 nên ta có số có dạng 6 x k + 4 - 3 hay 6 x k + 1 chia hết cho 5 .
Nhận thấy số 6 x k + 1 chia hết cho 5 là số nhỏ nhất khi k nhỏ nhất thỏa mãn. Dễ tìm được k = 4.
Suy ra số tiền ít nhất có trong túi thỏa mãn đề bài là 6 x 4 + 4 = 28 đồng.
Số tiền này khi chia đều cho 7 người thì mỗi người sẽ được 4 đồng và không còn dư đồng nào.
Trên đây là cách giải dựa theo đáp án gốc . Độc giả đã đưa ra một cách làm khác được nhiều người ủng hộ và đánh giá cao như sau :
Giả sử ngoài số tiền ban đầu , trong túi tiền có thêm hai đồng nữa thì số tiền mới sẽ chia hết cho cả 5 và 6 , hay nói cách khác số tiền mới là bội chung nhỏ nhất của 5 và 6 . Suy ra số tiền mới là 30 đồng .
Lúc này , chỉ cần bỏ đi hai đồng đã cho thêm vào sẽ ra số tiền trong túi ban đầu thỏa mãn đề bài là 28 .
Số tiền này khi chia đều cho 7 người sẽ không dư đồng nào .
Cảm ơn các bạn nhiều nha vì đã trả lời câu đố của mình ( nhất là bạn Song tử .... Tn(siêu quậy) đó , cảm ơn bạn nhiều vì sự nhanh trí và nhanh nhẹn của bạn ! ) . Chúc các bạn một mùa hè vui vẻ , sáng tạo và cũng chỉ còn 1 , 2 tháng nữa thôi là vào năm học mới ( nhiệm kỳ 2019 - 2020 ) rồi nên mình xin chúc các bạn học thật giỏi và có một năm học thành công , đáng nhớ !









\(C=\left(x^2-1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^4-1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^8-1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^{16}-1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^{32}-1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=x^{64}-1-x^{64}\)
\(C=-1\)
Vậy gtri của C không phụ thuộc vào x