NH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 4 2016
Ta coa : tam giác ABD vuông tại A
AB^2 + AD^2= BD^2 ( định lý pitago)
AD^2= BD^2 - AB^2 (1)
Ta có tam giác ADC vuông tại D
AD^2 + DC^2 = AC^2 ( định lý pitago)
AD^2 = AC^2 - DC^2 (2)
Từ (1) và (2) ta có:
BD^2 - AB^2 = AC^2- DC^2
DC^2 - AB^2 = AC^2 - BD^2
10 tháng 7 2019
Bài 1)
Trên AD lấy E sao cho AE = AB
Xét ∆ACE và ∆ACB ta có :
AC chung
DAC = BAC ( AC là phân giác)
AB = AE (gt)
=> ∆ACE = ∆ACB (c.g.c)
=> CE = CB (1)
=> AEC = ABC = 110°
Mà AEC là góc ngoài trong ∆EDC
=> AEC = EDC + ECD ( Góc ngoài ∆ bằng tổng 2 góc trong không kề với nó)
=> ECD = 110 - 70
=> EDC = 40°
Xét ∆ EDC :
DEC + EDC + ECD = 180 °
=> CED = 180 - 70 - 40
=> CED = 70°
=> CED = EDC = 70°
=> ∆EDC cân tại C
=> CE = CD (2)
Từ (1) và (2) :
=> CB = CD (dpcm)
b) Ta có thể thay sao cho tổng 2 góc đối trong hình thang phải = 180°
HN
1
HB
19 tháng 11 2018
Vẽ BO vuông góc AC tại O
DO phải cắt một trong 2 đoạn thẳng DC,DA. Giả sử BO cắt CD
Trên BO lấy E sao cho CD=CE
Tứ giác ABCE có:
AB2+CE2=BC2+AE2AB2+CE2=BC2+AE2
⇒AB2+CD2=BC2+AE2⇒AB2+CD2=BC2+AE2
Mà ⇒AB2+CD2=BC2+AD2⇒AB2+CD2=BC2+AD2
⇒D≡E⇒D≡E
⇒⇒ BD vuông góc AC.
⇒SABCD=BD.AC2⇒SABCD=BD.AC2
Nếu BD.AC2=AC2+BD24⇔(AC−BD)2=0BD.AC2=AC2+BD24⇔(AC−BD)2=0
Đẳng thức này chỉ xảy ra khi AC=BD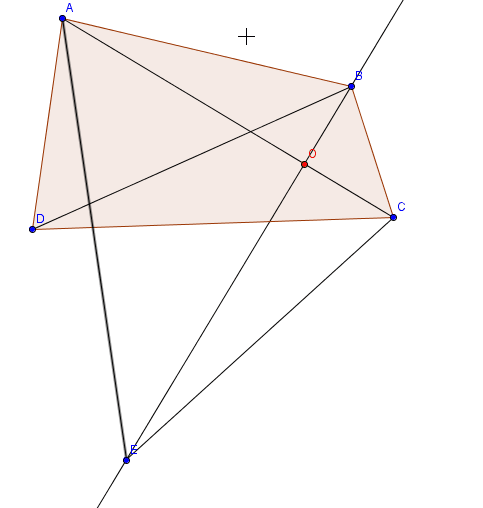
Kéo dài DA và CB lần lượt về phía A và B cắt nhau tại E
Xét tam giác DCE có \(\widehat{DEC}\) = 1800 - (\(\widehat{EDC}\) + \(\widehat{ECD}\)) = 1800- 900 = 900
⇒\(\Delta\)DEC vuông tại E
Xét \(\Delta\)AEB Theo pytago ta có: AE2 + BE2 = AB2
Tương tự ta có: DE2 + CE2 = DC2
Cộng vế với vế ta có: AE2 + BE2 + DE2 + CE2 = AB2+DC2
AE2 + CE2+BE2+DE2 = AB2+DC2 (1)
Xét \(\Delta\)AEC theo pytago ta có: AE2+ CE2 = AC2
Tương tự ta có: BE2 + DE2 = BD2
Cộng vế với vế ta có: AE2 + CE2 + BE2+ DE2 = AC2 + BD2 (2)
Từ (1) và (2) ta có: AC2 + BD2 = AB2 + DC2(đpcm)