K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
18 tháng 5 2019
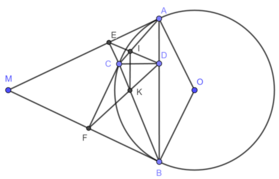

( góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BC)


CM
13 tháng 8 2019
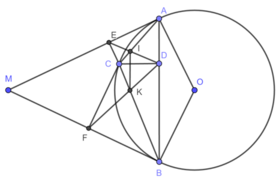

(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AC) (2)

(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung CB) (5)

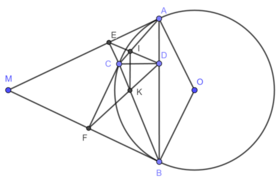

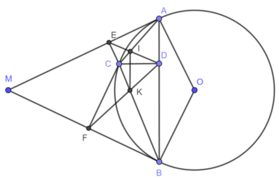

Lời giải:
a)
\(CD\perp AB, CE\perp AM, CF\perp MB\Rightarrow \left\{\begin{matrix} \widehat{CDA}=\widehat{CEA}=90^0\\ \widehat{CFB}=\widehat{CDB}=90^0\end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} \widehat{CDA}+\widehat{CEA}=180^0\\ \widehat{CFB}+\widehat{CDB}=180^0\end{matrix}\right.\)
Tứ giác $AECD$ và $BFCD$ có tổng hai góc đối bằng $180^0$ nên là tứ giác nội tiếp.
b)
Từ kết quả 2 tứ giác nội tiếp trên, kết hợp với tính chất góc tạo bởi tiếp tuyến và dây cung thì bằng góc nội tiếp chắn dây cung đó ta có:
\(\widehat{CDF}=\widehat{CBF}=\widehat{CAB}=\widehat{CAD}=\widehat{CED}\)
\(\widehat{CFD}=\widehat{CBD}=\widehat{CBA}=\widehat{EAC}=\widehat{CDE}\)
Do đó \(\triangle CDF\sim \triangle CED(g.g)\)
\(\Rightarrow \frac{CD}{CF}=\frac{CE}{CD}\Rightarrow CD^2=CE.CF\)
c)
Theo phần b:
\(\widehat{IDK}=\widehat{CDF}+\widehat{CDE}=\widehat{EAC}+\widehat{FBC}\)
\(=\widehat{CBA}+\widehat{CAB}=180^0-\widehat{ACB}=180^0-\widehat{ICK}\)
\(\Rightarrow \widehat{IDK}+\widehat{ICK}=180^0\)
Do đó tứ giác $ICKD$ nội tiếp.