Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

△DMC vuông tại D => DC2= MC2 - MD2
△AME vuông tại E => EA2 = AM2 - ME2
△BMF vuông tại F => BF2 = BM2 - MF2
Suy ra DC2 + EA2 + BF2 = MC2 - MD2 + AM2 - ME2 + BM2 - MF2 (1)
△BDM vuông tại D => BD^2 = BM^2 - MD^2
△CME vuông tại E => CE^2 = MC^2 - ME^2
△AMF vuông tại F => AF^2 = AM^2 - MF^2
Suy ra BD2 + CE2 + AF2 = BM2 - MD2 + MC2 - ME2 + AM2 - MF2 (2)
Từ (1) và (2) => BD2 + CE2 + AF2 = DC2 + EA2 + FB2

Các bạn học sinh KHÔNG ĐƯỢC đăng các câu hỏi không liên quan đến Toán, hoặc các bài toán linh tinh gây nhiễu diễn đàn. Online Math có thể áp dụng các biện pháp như trừ điểm, thậm chí khóa vĩnh viễn tài khoản của bạn nếu vi phạm nội quy nhiều lần.
Chuyên mục Giúp tôi giải toán dành cho những bạn gặp bài toán khó hoặc có bài toán hay muốn chia sẻ. Bởi vậy các bạn học sinh chú ý không nên gửi bài linh tinh, không được có các hành vi nhằm gian lận điểm hỏi đáp như tạo câu hỏi và tự trả lời rồi chọn đúng.
Mỗi thành viên được gửi tối đa 5 câu hỏi trong 1 ngày
Các câu hỏi không liên quan đến toán lớp 1 - 9 các bạn có thể gửi lên trang web h.vn để được giải đáp tốt hơn

△DMC vuông tại D => DC2= MC2 - MD2
△AME vuông tại E => EA2 = AM2 - ME2
△BMF vuông tại F => BF2 = BM2 - MF2
Suy ra DC2 + EA2 + BF2 = MC2 - MD2 + AM2 - ME2 + BM2 - MF2 (1)
△BDM vuông tại D => BD^2 = BM^2 - MD^2
△CME vuông tại E => CE^2 = MC^2 - ME^2
△AMF vuông tại F => AF^2 = AM^2 - MF^2
Suy ra BD2 + CE2 + AF2 = BM2 - MD2 + MC2 - ME2 + AM2 - MF2 (2)
Từ (1) và (2) => BD2 + CE2 + AF2 = DC2 + EA2 + FB2

A B C M D F E
Kí hiệu như trên hình.
Ta có : \(AF^2+MF^2=AE^2+EM^2=AM^2\)
\(BD^2+MD^2=BF^2+MF^2=BM^2\)
\(ME^2+EC^2=MD^2+DC^2=MC^2\)
Cộng các đẳng thức trên theo vế
\(\left(BD^2+CE^2+AF^2\right)+\left(MF^2+MD^2+ME^2\right)=\left(DC^2+EA^2+FB^2\right)+\left(EM^2+MF^2+MD^2\right)\)
\(\Rightarrow BD^2+CE^2+AF^2=DC^2+EA^2+FB^2\)

Trên tia đối của tia BA lấy I sao cho BI = DQ
\(\Delta DCQ=\Delta BCI\left(c.g.c\right)\Rightarrow\hept{\begin{cases}CQ=CI\\\widehat{DCQ}=\widehat{BCI}\end{cases}}\)
Ta có: \(\widehat{QCI}=\widehat{QCB}+\widehat{BCI}=\widehat{QCB}+\widehat{DCQ}=\widehat{BCD}=90^0\)
Ta có: \(AP+AQ+PQ=2AB\)
\(\Rightarrow AP+AQ+PQ=AP+PB+AQ+QD\)
\(\Rightarrow PQ=PB+QD\)
\(\Rightarrow PQ=PB+BI\Rightarrow PQ=PI\)
\(\Delta PCQ=\Delta PCI\left(c.c.c\right)\Rightarrow\widehat{PCQ}=\widehat{PCI}=\frac{\widehat{QCI}}{2}=\frac{90^0}{2}=45^0\)
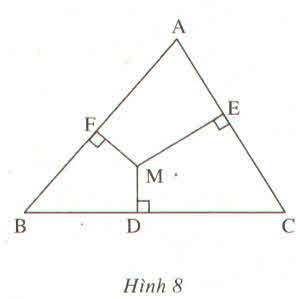
Bài 2. A B C M D E F
Áp dụng định lí Pytago ta có :
\(AM^2=AF^2+FM^2=AE^2+ME^2\)
\(BM^2=BD^2+MD^2=MF^2+BF^2\)
\(MC^2=ME^2+EC^2=MD^2+DC^2\)
\(\Rightarrow AF^2+FM^2+BD^2+MD^2+ME^2+EC^2=AE^2+ME^2+MF^2+BF^2+MD^2+DC^2\)
\(\Rightarrow BD^2+CE^2+AF^2=DC^2+EA^2+FB^2\)
bn giúp mk bài 1 đc k Ngọc