Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì OM ⊥ AB và ON ⊥ CD, mà AB // CD nên suy ra M, O, N thẳng hàng.
Mặt khác, do AB // CD nên theo Định lí Ta-lét ta có:
Từ đó, theo tính chất của dãy tỉ số bằng nhau, ta có:

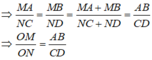

Từ O kẻ đường thẳng song song với AB và CD cắt AD tại E, cắt BC tại F.
Áp dụng kết quả chứng minh ở bài 14 ta có:
OE = OF
Từ đó, ta có:
S A E O = S B F O (1) (hai tam giác có cùng đường cao và hai đáy bằng nhau);
S D E O = S C F O (2)
Từ (1) và (2) suy ra : S O A D = S O B C (3)
Suy ra: OH.AD = OK.BC
⇔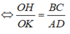

1: Xét ΔADC có OM//DC
nên \(\dfrac{OM}{DC}=\dfrac{AM}{AD}\left(1\right)\)
Xét ΔBDC có ON//DC
nên \(\dfrac{ON}{DC}=\dfrac{BN}{BC}\left(2\right)\)
Xét hình thang ABCD có MN//AB//CD
nên \(\dfrac{AM}{MD}=\dfrac{BN}{NC}\)
=>\(\dfrac{MD}{AM}=\dfrac{CN}{NB}\)
=>\(\dfrac{MD+AM}{AM}=\dfrac{CN+NB}{NB}\)
=>\(\dfrac{AD}{AM}=\dfrac{CB}{BN}\)
=>\(\dfrac{AM}{AD}=\dfrac{NB}{BC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{OM}{DC}=\dfrac{ON}{DC}\)
=>OM=ON

"Hai đường chéo cắt nhau tại O và song song với đáy AB....". Câu này không đúng lắm. Bạn xem lại đề.

Bài 1:
A B C M N O
Ta có BM là đường trung tuyến
⇒ \(\dfrac{OM}{OB}=\dfrac{1}{2}\)
CN là đường trung tuyến
⇒ \(\dfrac{ON}{OC}=\dfrac{1}{2}\)
Suy ra: \(\dfrac{OM}{OB}=\dfrac{ON}{OC}\Rightarrow OM.OC=ON.OB\)
...