Question

[Lê Thị Thùy Linh]

Bài 1:Cho ​​tam giác ABC đường thẳng qua A song song với BC cắt đường thẳng qua C song song với AB ở D.Gọi M là giao ddierm của BD và AC

a,Chứng minh tam giác ABC=tam giác CDA

b,Chứng minh M là trung điểm của AC

c,Đường thẳng d đi qua M cắt các đoạn thẳng AD,BC lần lượt tại I,K.Chứng minh M là trung điểm của IK 

Answer 1

[Kuroba Kaito]

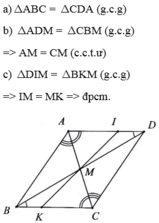
A B C M D I K

a) Do AD // BC (gt) => góc DAC = góc ACB (so le trong)

        AB // CD (gt) => góc BAC = góc ACD (so le trong)

Xét t/giác ABC và t/giác CDA

có góc ACB = góc DAC (cmt)

 AC : chung

 góc BAC = góc ACD (cmt)

=> t/giác ABC = t/giác CDA (g.c.g)

b) Ta có : t/giác ABC = t/giác CDA (cmt)

=> AB = CD (hai cạnh tương ứng)

Do AB // CD (gt) => góc ABD = góc BDC (so le trong)

Xét t/giác AMB và t/giác CMD

có góc BAM = góc  MCD (cmt)

  AB = CD (cmt)

  góc ABM = góc BDM (cmt)

=> t/giác AMB = t/giác CMD (g.c.g)

=> AM = MC (hai cạnh tương ứng)

=> M là trung điểm của AC

c) Xét t/giác AMI và t/giác CMK

có góc DAC = góc ACK (cmt)

    AM = CM (cmt)

   góc IMA = góc CMK (đối đỉnh)

=> t/giác AMI = t/giác CMK (g.c.g)

=> MI = MK (hai cạnh tương ứng)

=> M là trung điểm của IK

Answer 2

[jibe thinh]

Kuroba Kaito, mình đã biết I, M, K có thẳng hàng đâu. mới chứng minh được MI=Mk nên chưa thể nói M là trung điểm của IK được