Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{1}{a}-\frac{1}{b}=\frac{1}{a-b}\)
\(\Leftrightarrow\frac{b-a}{ab}=\frac{1}{a-b}\)
\(\Leftrightarrow\frac{\left(b-a\right)\left(a-b\right)}{ab\left(a-b\right)}=\frac{ab}{\left(a-b\right)ab}\)
\(\Leftrightarrow-\left(b-a\right)^2=ab\)
\(\Leftrightarrow-b^2+2ab-a^2=ab\)
\(\Leftrightarrow\)\(ab=a^2+b^2\)
Từ đây dùng cô-si : \(a^2+b^2\ge4ab\)
Vậy không có số dương a,b thỏa mãn

Bài 1 :
Ta có :
\(\dfrac{1}{a}-\dfrac{1}{b}=\dfrac{1}{a-b}\Rightarrow\dfrac{b-a}{ab}=\dfrac{1}{a-b}\)
\(\Rightarrow\left(b-a\right)\left(a-b\right)=ab.1\Rightarrow-\left(a-b\right)\left(a-b\right)=ab\)
\(\Rightarrow-\left(a-b\right)^2=ab\)
Vì \(-\left(a-b\right)^2\le0\) với mọi a, b ko thể cùng dương
Vậy ko tồn tại 2 số dương a,b khác nhau để thõa mãn đề bài
Bài 1:
Trường hợp 1 :
Giả sử a > b > 0 \(=>\) \(\dfrac{1}{a}< \dfrac{1}{b}=>\dfrac{1}{a}-\dfrac{1}{b}< 0\) ; \(\dfrac{1}{a-b}>0\)
\(=>\dfrac{1}{a}-\dfrac{1}{b}\ne\dfrac{1}{a-b}\)
Trường hợp 2 :
Giả sử a < b \(=>\dfrac{1}{a}>\dfrac{1}{b}=>\dfrac{1}{a}-\dfrac{1}{b}>0\) ; \(\dfrac{1}{a-b}< 0\)
\(=>\dfrac{1}{a}-\dfrac{1}{b}\ne\dfrac{1}{a-b}\)
Vậy không tồn tại hai số nguyên dương a và b khác nhau sao cho \(\dfrac{1}{a}-\dfrac{1}{b}=\dfrac{1}{a-b}\)

1. a chia het cho 20 va 12 suy ra a chia het cho 2;3;4;5.
vi 2
2 . 3 =6; 2 .4 =8
suy ra a chia 20 ko the du 8
a chia 12 ko the du 6
2.
=4a - 4b + 7b
=4 . [a - b] + 7b
a - b chia het cho 7 ; 7b chia het cho 7 suy ra 4a + 3b chia het cho 7
3.
a 3n - 3 + chia het n -1
3[n - 1] + 7 chia het n - 1
vi 3[n - 1]chia het chgo 7 suy ra 7 chia het n -1
vay n = 8

Bài 13 :
Có : c = (a-b).[-(a-b)] = -(a-b)^2
Vì a khác b => a-b khác 0 => (a-b)^2 > 0
=> c = -(a-b)^2 < 0
=> c là số âm
Tk mk nha

Ta có:
a=1\(\dfrac{1}{2}\).b
=>a-b= \(1\dfrac{1}{2}\)b-b
a-b=\(\dfrac{1}{2}\)b
=> 8=\(\dfrac{1}{2}\)b
=>b=8:\(\dfrac{1}{2}\)=16
=>a=16+8=24
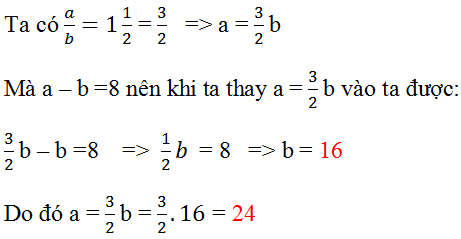
Giả sử a > b > 0 \(=>\frac{1}{a}< \frac{1}{b}=>\frac{1}{a}-\frac{1}{b}< 0;\frac{1}{a-b}>0\)
\(=>\frac{1}{a}-\frac{1}{b}\ne\frac{1}{a-b}\)
Trường hợp 2
Giả sử a < b \(=>\frac{1}{a}>\frac{1}{b}=>\frac{1}{a}-\frac{1}{b}>0;\frac{1}{a-b}< 0\)
\(=>\frac{1}{a}-\frac{1}{b}\ne\frac{1}{a-b}\)
Vậy không tồn tại hay không có hai số nguyên dương a , b khác nhau sao cho \(\frac{1}{a}-\frac{1}{b}=\frac{1}{a-b}\)
\(a-b=2\left(a+b\right)=\frac{a}{b}\)
\(\hept{\begin{cases}a-b=2\left(a+b\right)\\2\left(a+b\right)=\frac{a}{b}\end{cases}}\)
a-b=2(a+b)
a-b=2a+2b
3b=a
Another way :
a-b=2(a+b)
=> -2b - b -2a + a =0
-(3b+a)=0
3b+a=0
Do đó :3b-b= 3b/b = 3 nên b = 3/4
b = 3/4 nên a = - 9/4
\(\Leftrightarrow\hept{\begin{cases}b=\frac{3}{4}\\a=-\frac{9}{4}\end{cases}}\)