Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(M=\left[\left(\frac{2}{193}-\frac{3}{386}\right).\frac{193}{17}+\frac{33}{34}\right]:\left[\left(\frac{7}{2001}+\frac{11}{4002}\right).\frac{2001}{25}+\frac{9}{2}\right] \)
\(=\left(\frac{2}{17}-\frac{3}{34}+\frac{33}{34}\right):\left(\frac{7}{25}+\frac{11}{50}+\frac{9}{2}\right)\)
\(=\frac{4-3+33}{34}:\frac{14+11+225}{50}=1:5=0.2\)

Ta có
\(M=\left[0,8\times7+\left(0,8\right)^2\right]\times\left(1,25\times7-\frac{4}{5}\times125\right)+31,64\):\(M=\left[\frac{28}{5}+\frac{16}{25}\right]\times\left(\frac{35}{4}-1\right)+31,64\)\(=\frac{156}{25}\times\frac{31}{4}+31,64\)\(=48,36+31,64=80\)
và \(B=\frac{\left(1,09-0,29\right)\times\frac{5}{4}}{\left(18,9-16,65\right)\times\frac{8}{9}}=\frac{\frac{4}{5}\times\frac{5}{4}}{\frac{9}{4}\times\frac{8}{9}}=\frac{1}{2}=0,5\)
M gấp: \(80:0,5=160\)lần B
k đúng nha

Ta có :
A = \(\left[0,8.7+\left(0,8\right)^2\right].\left(1,25.7-\dfrac{4}{5}.1,25\right)+31,64\)
A = \(\left[0,8.\left(7+0,8\right)\right].\left[1,25.\left(7-\dfrac{4}{5}\right)\right]+31,64\)
A = \(\left(0,8.7,8\right)\left(1,25.6,2\right)+31,64\)
A = 6,24 . 7,75 + 31,64
A = 48,36 + 31,64
A = 80
B = \(\dfrac{\left(1,09-1,29\right).\dfrac{5}{4}}{\left(18,9-16,25\right).\dfrac{8}{9}}\)
B= \(\dfrac{\dfrac{4}{5}.\dfrac{5}{4}}{\dfrac{9}{4}.\dfrac{8}{9}}\)
B = \(\dfrac{1}{2}\)
Vậy A gấp B : 80 :\(\dfrac{1}{2}\) = 160 (lần)

\(M=\left[\dfrac{4-3}{386}\cdot\dfrac{193}{17}+\dfrac{33}{34}\right]:\left[\dfrac{14+11}{4002}-\dfrac{2001}{25}+\dfrac{9}{2}\right]\)
\(=\left(\dfrac{1}{17}\cdot\dfrac{193}{386}+\dfrac{33}{34}\right):\left[\dfrac{25}{4002}-\dfrac{2001}{25}+\dfrac{9}{2}\right]\)
\(=1:\dfrac{625-2001\cdot4002+9\cdot50525}{100050}\)
\(=-\dfrac{100050}{7552652}\)
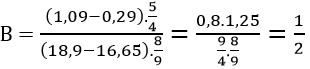
Bài 1:
Cách 1:
Ta có : x + y = xy
<=> x = xy - y
<=> x = y(x - 1)
<=> x/y = x - 1
<
V=> x + y = x - 1
=> y = -1
Có y = -1 , ta có thể tính được x :
Ta có :
x + y = xy
<=> x - 1 = -x
<=> 2x = 1
=> x = 1/2
Vậy x = 1/2 ; y = -1
Cách 2 : Tham khảo nhé :
xy = x/y <=> x = 0 hoặc y² = 1
TH1: x = 0
=> 0 + y = 0 <=> y = 0 (loại)
TH2: y = 1
=> x + 1 = x <=> 1 = 0 (loại)
TH3: y = -1
=> x - 1 = -x <=> x = 1/2
=> x = 1/2 và y = -1
Cách 3 :
x+y > 0 và 1/x + 1/y = (x+y)/xy > 0 => xy > 0 mà x+y > 0 => x > 0, y > 0
đặt x = a/b ; y = c/d với a, b, c, d nguyên dương; (a,b) = 1 ; (c,d) = 1
Có:
x+y = a/b + c/d = (ad+bc)/bd = m
1/x+1/y = b/a + d/c = (ad+bc)/ac = n ; với m, n nguyên dương
=> { ad + bc = mbd (1*)
---- { ad + bc = nac (2*)
*-* (2*) => d + bc/a = nc => bc chia hết cho a
mà a và b nguyên tố cùng nhau (hay kí hiệu là (a,b) = 1) nên c chia hết cho a
*-* (2*) => ad/c + b = na => ad chia hết cho c
lại có (d,c) = 1 nên a chia hết cho c
từ hai điều trên ta có a = c
*-* (1*) => ad/b + c = md => ad chia hết cho b
mà (a,b) = 1 nên d chia hết cho b
*-* (1*) => a + bc/d = mb => bc chia hết cho d
cũng có (c,d) = 1 nên b chia hết cho d
từ 2 điều trên (b chia hết cho d và d chia hết cho b) => b = d
từ đây ta có kết luận: x = a/b = c/d = y
ta ghi lại giả thiết:
x+y = 2x = 2(a/b) = m (1**)
1/x + 1/y = 2/x = 2(b/a) = n (2**)
lấy (1**) * (2**) => 4 = mn ; với m, n nguyên dương ta có các khã năng là:
* m = n = 2 => 2x = 1 => x = 1
* { m = 1 ; n = 4 => { 2x = 1 ; 2/x = 4 => x = 1/2
* { m = 4 ; n = 1 => { 2x = 4 ; 2/x = 1 => x = 2
tóm lại có 3 cặp số hữu tỉ (x, y) thỏa mản là: (1,1) ; (1/2, 1/2) ; (2,2)
Bài 2:
a) M=[(2/193−3/386).193/17+33/34]:[(7/2001+11/4002).2001/25+9/2]
=[(4/386−3/386).193/17+33/34]:[(14/4002+11/4002).2001/25+9/2]
=(1/193.2.193/17+33/34):(25/2.2001.2001/25+9/2)
=(1/34+33/34):(1/2+9/2)
=1:5=1/5