Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: v=54km/h=15m/s
Chọn chiều (+) là chiều chuyển động, gốc thời gian lúc bắt đầu hãm phanh.
Theo định luật II - Niutơn, ta có:
a → = F → m → a = − F m = − 3000 1000 = − 3 m / s 2
Mặt khác, ta có: v 2 − v 0 2 = 2 as
↔ 0 − 15 2 = 2. ( − 3 ) s → s = 37 , 5 m
Đáp án: A

Chọn D
Chọn chiều + là chiều chuyển động, gốc thời gian lúc bắt đầu hãm phanh.
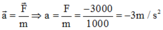
Ta có:
![]()

Chọn D
Chọn chiều + là chiều chuyển động, gốc thời gian lúc bắt đầu hãm phanh.
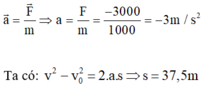

Chọn đáp án C
? Lời giải:
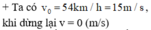
+ Chọn chiều dương là chiều chuyển động, gốc thời gian lúc bắt đầu hãm phanh. Theo định luật II Newton F → h = m a →


Đáp án B.
Chọn chiều + là chiều chuyển động, gốc thời gian lúc bắt đầu hãm phanh.
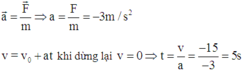

Giải: Chọn chiều dương là chiều chuyển động của tàu, gốc tọa độ tại vị trí hãm phanh, gốc thời gian lúc bắt đầu hãm phanh.
a. v 0 = 72 3 , 6 = 20 m / s ; v 1 = 54 3 , 6 = 15 m / s ; v 2 = 36 3 , 6 = 10 m / s
gia tốc chuyển động của tàu a = v 1 − v 0 Δ t = 15 − 20 10 = − 0 , 5 m / s 2
Mà v 2 = v 0 + a . t 2 ⇒ t 2 = v 2 − v 0 a = 10 − 20 − 0 , 5 = 20 s
Khi dừng lại hẳn thì v 3 = 0
Áp dụng công thức v 3 = v 0 + a t 3 ⇒ t 3 = v 3 − v 0 a = 0 − 20 − 0 , 5 = 40 s
b;Áp dụng công thức v 3 2 − v 0 2 = 2. a . S ⇒ S = v 3 2 − v 0 2 2. a = 400 m

Đổi 2 tấn = 2000 kg
36 km/h = 10 m/s
a. Gia tốc của xe là:
\(a=\dfrac{\Delta v}{t}=\dfrac{0-10}{2}=-5\) (m/s)
Độ lớn của lực hãm là:
\(\left|F\right|=\left|ma\right|=10000\) (N)
Hệ số ma sát giữa xe với mặt đường là:
\(\mu=\dfrac{F}{N}=\dfrac{10000}{20000}=0,5\)
b. Quãng đường xe đi được cho đến khi dừng lại là:
\(s=\dfrac{v^2}{2a}=\dfrac{10^2}{2.5}=10\) (m)
\(m\) = 1 tấn = 1000 kg.
\(v_0\) = 54 km/h = 15 m/s.
Ô tô chịu tác dụng của 2 lực là lực hút \(\overrightarrow{P}\) của Trái Đất và lực hãm \(\overrightarrow{F}\).
y x v F P O
Áp dụng định luật II Niu-tơn, ta có:
\(\overrightarrow{a}\) = \(\dfrac{\overrightarrow{P}+\overrightarrow{F}}{m}\) (*)
a. Chọn hệ trục xOy như hình vẽ.
Chiếu phương trình (*) lên trục Ox ta được:
\(a=\dfrac{-F}{m}=\dfrac{-300}{1000}=-0,3\) (m/s2)
Chiếu phương trình (*) lên trục Oy ta được:
\(a=0\) (Vì ô tô không chuyển động theo phương Oy)
Vậy gia tốc của ô tô là \(-0,3\) (m/s2).
Từ công thức liên hệ giữa vận tốc, gia tốc và quãng đường đi được:
\(v^{2^{ }}-v_0^2=2as\)
Suy ra quãng đường xe đi được cho đến khi dừng lại là:
\(s=\dfrac{v^2-v_0^2}{2a}=\dfrac{0^2-15^2}{2.\left(-0,3\right)}=375\left(m\right)\)
b. Quãng đường xe đi được cho đến khi dừng lại được tính theo công thức: \(s=v_0t+\dfrac{1}{2}at^2\)
Suy ra: \(375=15t+\dfrac{1}{2}.\left(-0,3\right)t^2\)
=> \(-\dfrac{3}{20}t^2+15t-375=0\)
=> \(t=50\left(s\right)\)
Vậy thời gian ô tô chuyển động cho đến khi dừng lại là 50s.