Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TH1: 0 sáng, 6 tối
=>Có 0,3^6
TH2: 1 ság, 5 tối
=>Có \(C^5_6\cdot0.3^5\cdot0.7^1\)
TH3: 2 sáng, 4 tối
=>Có \(C^4_6\cdot0.3^4\cdot0.7^2\)
=>P=0,07047

Xác suất để không thu được thông tin là \(0,35\)
a.
Xác suất để thu tín hiệu khi phát 5 lần:
\(P=1-0,35^5=...\)
b.
Gọi số lần phát tín hiêu là n thì:
\(0,35^n\le1-0,9985\)
\(\Rightarrow n\ge6,19\)
\(\Rightarrow\) Cần phát tín hiệu ít nhất 7 lần

Gọi A là biến cố "Tín hiệu phát ra là A"
B là biến cố "Tín hiệu phát ra là B"
\(A_1\) là biến cố "Tín hiệu thu được là A"
\(B_1\) là biến cố "Tín hiệu thu được là B"
Ta có hệ {A;B} là một hệ biến cố đầy đủ
\(P\left(A\right)=0,8\) ; \(P\left(B\right)=0,2\) ; \(P\left(B_1|A\right)=\dfrac{1}{5}\) ; \(P\left(A_1|B\right)=\dfrac{1}{8}\)
Áp dụng công thức xác suất đầy đủ:
\(P\left(A_1\right)=P\left(A\right).P\left(A_1|A\right)+P\left(B\right).P\left(A_1|B\right)=0,8.\left(1-\dfrac{1}{5}\right)+0,2.\dfrac{1}{8}=0,665\)
b.
\(P\left(A|A_1\right)=\dfrac{P\left(A\right).P\left(A_1|A\right)}{P\left(A_1\right)}=\dfrac{0,8.\left(1-\dfrac{1}{5}\right)}{0,665}=\dfrac{128}{133}\)

Đáp án : B
Với mỗi bóng đèn ta có hai sự lựa chọn trạng thái là bật hoặc tắt. Như vậy, theo quy tắc nhân sẽ có cách lựa chọn bật, tắt các bóng đèn đó.
Tuy nhiên có một trạng thái duy nhất là khi cả 10 bóng đèn đều tắt thì phòng không có ánh sáng. Vậy để phòng có ánh sáng thì có cách bật, tắt các bóng đèn.

1.
Không gian mẫu: \(8!\)
Xếp Quân Lâm cạnh nhau: \(2!\) cách
Coi cặp Quân-Lâm như 1 bạn, hoán vị với 6 bạn còn lại: \(7!\) cách
\(\Rightarrow2!.7!\) cách xếp thỏa mãn
Xác suất: \(P=\dfrac{2!.7!}{8!}=\dfrac{1}{4}\)
2.
Không gian mẫu: \(C_{12}^3\)
Lấy 3 bóng sao cho ko có bóng tốt nào (cả 3 đều là bóng ko tốt): \(C_4^3\) cách
\(\Rightarrow C_{12}^3-C_4^3\) cách lấy 3 bóng sao cho có ít nhất 1 bóng tốt
Xác suất: \(P=\dfrac{C_{12}^3-C_4^3}{C_{12}^3}=...\)
3.
Số tam giác bằng với số cách chọn 3 điểm từ 4 điểm nên có: \(C_4^3=...\) tam giác
4.
\(T_{\overrightarrow{v}}\left(E\right)=F\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}x=-3+1=-2\\y=5-2=3\end{matrix}\right.\) \(\Rightarrow\left(-2;3\right)\)
5.
Có 2 cạnh chéo nhau với AB là SC, SD

Chọn A
+ Chia đều 10 đội vào 2 bảng A và B có ![]() cách.
cách.
Do đó số phần tử của không gian mẫu là : ![]()
+ Sắp xếp đội của lớp 10A1 và 10A2 vào 2 bảng khác nhau A và B có 2! cách.
Chọn 4 đội trong 8 đội còn lại để xếp vào bảng có đội lớp 10A1 có C 8 4 cách.
Bốn đội còn lại xếp vào bảng còn lại.
Suy ra số cách chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau là ![]()
Gọi A là biến cố “Chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau ” thì số các kết quả thuận lợi cho biến cố A là: ![]()
+ Xác suất cần tìm là: 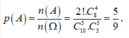

Chọn A.
Chọn ngẫu nhiên 5 học sinh trong số 48 học sinh có:![]()
- Gọi A là biến cố "chọn 5 học sinh trong đó có ít nhất một học sinh nữ" thì ![]() là biến cố "chọn 5 học sinh mà trong đó không có học sinh nữ".
là biến cố "chọn 5 học sinh mà trong đó không có học sinh nữ".
- Ta có số kết quả thuận lợi cho ![]() là:
là:
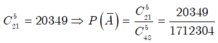
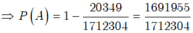

Gọi A: “Học sinh thích môn Bóng đá”
B: “Học sinh thích môn Bóng bàn”
Do đó ta có \(P\left( A \right) = \frac{{19}}{{30}},P\left( B \right) = \frac{{17}}{{30}},P\left( {AB} \right) = \frac{{15}}{{30}}\)
Theo công thức cộng xác suất
\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{{19}}{{30}} + \frac{{17}}{{30}} - \frac{{15}}{{30}} = \frac{{21}}{{30}} = \frac{7}{{10}}\)
Vậy xác suất để chọn được học sinh thích ít nhất một trong hai môn Bóng đá hoặc Bóng bàn là \(\frac{7}{{10}}\)
