Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

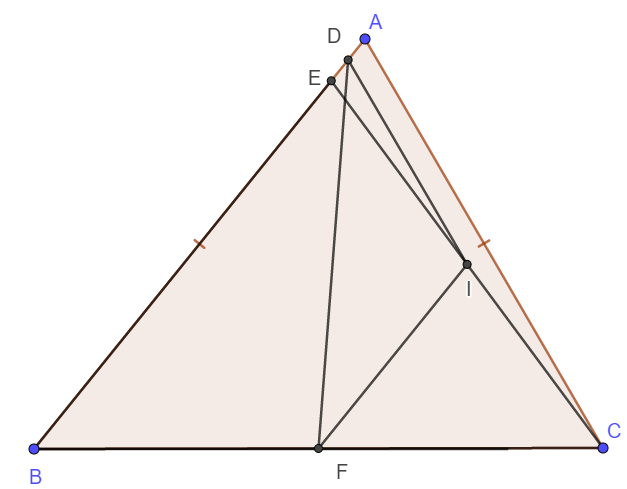
a) Xét tam giác ECB có I, F lần lượt là trung điểm của CE và CB nên IF là đường trung bình tam giác.
Suy ra \(IF=\frac{ED}{2}\)
Xét tam giác ECA có I, D lần lượt là trung điểm của CE và EA nên ID là đường trung bình tam giác.
Suy ra \(ID=\frac{AC}{2}\)
Mà AC = BE nên ID = IF
Vậy tam giác DIF cân tại I.
b) Do tam giác DIF cân tại I nên \(\widehat{FDI}=\widehat{DFI}\)
Lại có IF là đường trung bình tam giác BEC nên IF // AB, suy ra \(\widehat{DFI}=\widehat{FDB}\)
Từ đó ta có: \(\widehat{FDI}=\widehat{FDB}\Rightarrow\widehat{BDI}=2\widehat{IDF}\)
Cũng do DI là đường trung bình nên DI // AC hay \(\widehat{BDI}=\widehat{BAC}\)
Vậy nên \(\widehat{BAC}=2\widehat{IDF}\)

gợi ý câu a: dùng tính chất đường trung bình ta được (tự nêu 2 cặp bằng nhau)
ID là đường trung bình trong tam giác ACE \(\RightarrowÌF=AC\left(1\right)\)
IF là đường trung bình tronng tam giác CEB \(\Rightarrow IF=EB\left(2\right)\)
Mà \(AC=EB\left(3\right)\)
Từ (1),(2),(3) \(\Rightarrow ID=IF\)
Suy ra tam giác IDF cân tại I
câu b chưa làm đc

Em tham khảo tại đây nhé.
Câu hỏi của Trần Nam Anh - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo tại đây nhé.
Câu hỏi của Trần Nam Anh - Toán lớp 8 - Học toán với OnlineMath

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

Em tham khảo tại đây nhé.
Câu hỏi của Trần Nam Anh - Toán lớp 8 - Học toán với OnlineMath

Bạn tự vẽ hình nha
a) Vì D,E là trung điểm của AC và AB nên ED là đường trung bình của tam giác ABC.
Suy ra ED = \(\frac{BC}{2}\)= \(\frac{4}{2}\)= 2 (cm)
Tứ giác EDCB có ED // BC ( Vì ED là đường trung bình của tam giác ABC) nên EDCB là hình thang.
Vì M, N là trung điểm của EB và CD nên MN là đường trung bình của hình thang EDCB
suy ra MN = \(\frac{ED+BC}{2}\)= \(\frac{2+4}{2}\)=3 (cm).
Vậy MN =3 (cm)
b) Ta có MN// ED ( MN là đương tb củahình thang EDCB) nên MP//ED , QN//ED
Xét tg EBD có MP//ED (cmt)
MB =ME (gt)
Suy ra P là trung điểm của BD ,nên MP là đương tb của tg EBD nên MP= \(\frac{ED}{2}\)=\(\frac{2}{2}\)= 1(cm).
Chứng minh tương tự với tg ECD cũng có QN = 1(cm)
Ta có MN = MP + PQ +QN
3 = 1+PQ +1
QN =1 (cm)
Nên MP=PQ=QN.(đpcm)
Có nhìu chỗ thiếu xót mong mấy bạn thông cảm.
Bài 2:
a: Xét hình thang ABCD có
N là trung điểm của AD
M là trung điểm của BC
Do đó: NM là đường trung bình
=>NM//AB//CD
=>NM\(\perp\)AD
Xét ΔMAD có
MN là đường cao
MN là đường trung tuyến
Do đó: ΔMAD cân tại M
b: Ta có: \(\widehat{MAB}+\widehat{MAD}=90^0\)
\(\widehat{MDC}+\widehat{MDA}=90^0\)
mà \(\widehat{MAD}=\widehat{MDA}\)
nên \(\widehat{MAB}=\widehat{MDC}\)