Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x x` y y` O A B t t` C u v D a các tia đối nhau là: aA và Ay; xA và Ax` các tia trùng nhau là: xO và xA; xO và xx`; xA và xx` aA và aC; aA và aC; aA và aB; aA và ay;AC và AB; AC và AB AC và Ay; CB và Cy

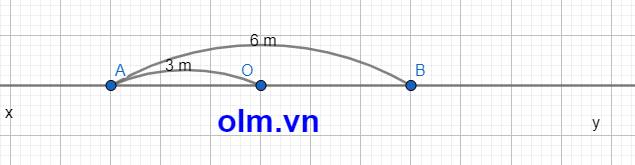
a, Các cặp tia đối nhau chung gốc A lần lượt là:
Ax và AO; Ax và AB; Ax và AY
b, Vì OA và OB là hai tia đối nhau nên O nằm giữa A và B
⇒ OA + OB = AB
⇒ OB = AB - OA
Độ dài đoạn OB là: 6 - 3 = 3 (cm)
c, Vì O nằm giữa A và B mà OA = OB = 3 cm nên O là trrung điểm AB

a: Các cặp tia đối nhau gốc A là:
AB,Ax
AO,Ax
Ay,Ax
b: Trên tia Ay, ta có: AO<AB(3cm<6cm)
nên O nằm giữa A và B
=>AO+OB=AB
=>OB+3=6
=>OB=3(cm)
c: Vì O nằm giữa A và B
và OA=OB(=3cm)
nên O là trung điểm của AB
a) Cặp tia đối nhau gốc A trên hình vẽ là tia OA và tia AO.
b) Độ dài đoạn thẳng OB có thể tính bằng cách sử dụng định lý Pythagoras trong tam giác vuông OAB:
OB² = OA² + AB²
OB² = 3² + 6²
OB² = 9 + 36
OB² = 45
OB = √45 ≈ 6.71 cm
c) Điểm O không phải là trung điểm của đoạn thẳng AB. Để chứng minh điều này, ta có thể tính độ dài của OA và OB:
OA = 3 cm
OB = 6.71 cm
Ta thấy OA ≠ OB, do đó O không là trung điểm của AB.
tick mik nha

a) Vì \(MOP-MOQ\) là hai góc kề bù, ta có :
\(MOQ=180^0_{ }-MOP=180^0_{ }-70^0_{ }\)
\(\Rightarrow MOQ=110^0_{ }\)
Áp dụng tính chất hai góc đối đỉnh, ta có :
\(MOP=NOQ\)
\(MOQ=PON\)
b) Vì \(Ot\) là tia phân giác của \(MOP\Rightarrow TOP=TOM=\frac{1}{2}MOP=\frac{110}{2}=55^0_{ }\)
Vì \(POT-QOT'\) là hai góc đối đỉnh \(\Rightarrow POT=QOT'=55^0_{ }\left(1\right)\)
Vì \(MOT-NOT'\)là hai góc đối đỉnh \(\Rightarrow MOT=NOT'=55^0_{ }\left(2\right)\)
Từ \(\left(1\right)-\left(2\right)\Rightarrow OT'\)là tia phân giác của \(NOQ\)
c) \(POT-QOT'\)
\(MOT-NOT'\)
\(POM-NOQ\)