Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét 2 tam giác ADB và BCD có:
góc DAB = góc DBC (gt)
góc ABD = góc BDC ( so le trong )
nên tam giác ADB đồng dạng với tam giác BDC.(1)
b) Từ (1) ta được AB/BC = DB/CD = AB/BD
hay ta có; AD/BC = AB/BD <==> 3,5/BC = 2,5/5
==> BC= 3,5*5/2,5 = 7 (cm)
ta cũng có: DB/CD = AB/BD <==> 5/CD = 2,5/5
==> CD = 5*5/2,5 =10 (cm)
c) Từ (1) ta được;
AD/BC = DB/CD = AB/BD hay 3.5/7 = 5/10 = 2,5/5 = 1/2 .
ta nói tam giác ADB đồng giạc với tam giác BCD theo tỉ số đồng dạng là 1/2
mà tỉ số diện tích bằng bình phương tỉ số động dạng
do đó S ADB/ S BCD = (1/2)^2 = 1/4

Bài 22 :
Vì ABCD là hình bình hành
=> AB = DC
Mà M là trung điểm AB
=> AM = MB
Mà N là trung điểm DC
=> DN = NC
=> AM = DN
Mà AB//DC
=> DN//AM
=> AMND là hình bình hành
Chứng minh tương tự ta có : MBCN là hình bình hành

Bài 2:
a: Xét ΔABE và ΔACF có
góc ABE=góc ACF
AB=AC
góc A chung
Do đó: ΔABE=ΔACF
Suy ra: AE=AF
b: Xét ΔABC có AF/AB=AE/AC
nên FE//BC
=>BFEC là hình thang
mà CF=BE
nên BFEC là hình thang cân
c: Xét ΔFEB có góc FEB=góc FBE
nên ΔFEB cân tại F
=>FE=FB=EC

Bài 1:
Ta có:góc ABD=góc CBD
góc ECB=góc AEC
Mà góc B = góc C
suy ra góc ABD = góc CBD = góc ECB=gócACE
Ta lại có:góc B = góc C
=> BEDC là hình thang cân=>BC//DE
=>BE=DCvà BD=CE
Mà tam giác ABC cân tại A=>AE=AD
Vì góc DBC= góc EDB(so le trong)
Mà ABD=DBC=>góc ABD= góc DBC=>tam giác EBD cân tai E
=>EB=EDmà EB=DC
=>ED=EB=DC.đpcm
Bài 2:
Ta có :
góc ACD=góc BDC
=>ABCD là HTC(định nghĩa hình thang cân)

A B E C D 1 1
a) Hình thang ABEC ( AB // CE ) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó \(\Delta BDE\)cân
b) Do AC // BE nên \(\widehat{E}=\widehat{C_1}\left(3\right)\)
Mà tam giác BDE cân tại B ( câu a ) nên \(\widehat{E}=\widehat{D_1}\left(4\right)\)
Từ (3)(4) => \(\widehat{D_1}=\widehat{C_1}\)
* Xét 2 tam giác : ACD và BDC có :
DC chung
AC = BD ( gt )
\(\widehat{C_1}=\widehat{D_1}\left(cmt\right)\)
\(\Rightarrow\Delta ACD=\Delta BDC\left(c-g-c\right)\)
c) Theo ( c/m câu b ) ta có :
\(\Delta ACD=\Delta BDC\)
nên \(\widehat{ADC}=\widehat{BCD}\)( 2 góc tương ứng )
Vậy hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.

Bài 2:
a: Xét ΔABE và ΔACF có
góc ABE=góc ACF
AB=AC
góc A chung
Do đó: ΔABE=ΔACF
Suy ra: AE=AF
b: Xét ΔABC có AF/AB=AE/AC
nên FE//BC
=>BFEC là hình thang
mà CF=BE
nên BFEC là hình thang cân
c: Xét ΔFEB có góc FEB=góc FBE
nên ΔFEB cân tại F
=>FE=FB=EC

Bài giải:
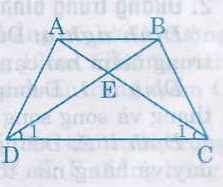
Gọi E là giao điểm của AC và BD.
∆ECD có \(\widehat{C_1}=\widehat{D}\) (do \(\widehat{ACD}=\widehat{BDC}\)) nên là tam giác cân.
Suy ra EC = ED (1)
Tương tự EA = EB (2)
Từ (1) và (2) suy ra AC = BD
Hình thang ABCD có hai đường chéo bằng nhau nên là hình thang cân.

cho tứ giác abcd có ad=ab=bc và gốc Á+góc C=180.CMR a)tia DB là tia phân giác của góc ADC.b) Tứ giác ABCD là hình thang cân
a, Xet tu giac ABCD co \(\widehat{BAC}+\widehat{BCD}=180° \)→Tu giac ABCD la tu giac noi tiep\(→\hept{\begin{cases}\widehat{CAB}=\widehat{BDC}\\\widehat{ADB}=\widehat{ACB}\end{cases}}\)
Mat khac do AB=BC nen tam giac ABC can suy ra \(\widehat{CAB}=\widehat{ACB}\)
Tu day ta co \(\widehat{BCD}=\widehat{ADB}\)hay DB la phan giac cua \(\widehat{ADC}\)