Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

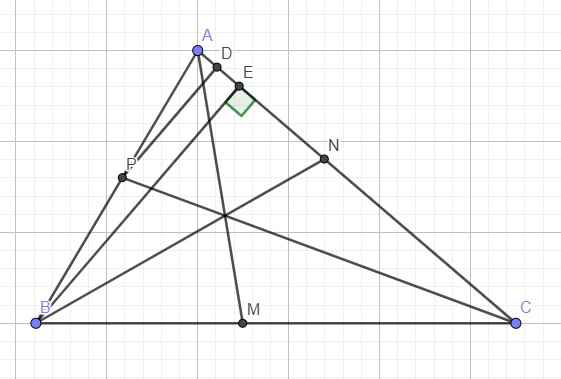
Kẻ PD và BE vuông góc AC
Định lý phân giác: \(\dfrac{AN}{NC}=\dfrac{AB}{BC}\Rightarrow\dfrac{AN}{AN+NC}=\dfrac{AB}{AB+BC}\Rightarrow\dfrac{AN}{AC}=\dfrac{AB}{AB+BC}=\dfrac{c}{a+c}\)
Tương tự: \(\dfrac{AP}{AB}=\dfrac{b}{a+b}\)
Talet: \(\dfrac{PD}{BE}=\dfrac{AP}{AB}\)
\(\dfrac{S_{APN}}{S_{ABC}}=\dfrac{\dfrac{1}{2}PD.AN}{\dfrac{1}{2}BE.AC}=\dfrac{AP}{AB}.\dfrac{AN}{AC}=\dfrac{bc}{\left(a+b\right)\left(a+c\right)}\)
Tương tự: \(\dfrac{S_{BPM}}{S_{ABC}}=\dfrac{ac}{\left(a+b\right)\left(b+c\right)}\) ; \(\dfrac{S_{CMN}}{S_{ABC}}=\dfrac{ab}{\left(a+c\right)\left(b+c\right)}\)
\(\Rightarrow\dfrac{S_{APN}+S_{BPM}+S_{CMN}}{S_{ABC}}=\dfrac{bc}{\left(a+b\right)\left(a+c\right)}+\dfrac{ac}{\left(a+b\right)\left(b+c\right)}+\dfrac{ab}{\left(a+c\right)\left(b+c\right)}\)
\(\Rightarrow\dfrac{S_{MNP}}{S_{ABC}}=\dfrac{S_{ABC}-\left(S_{APN}+S_{BPM}+S_{CMN}\right)}{S_{ABC}}=1-\left(\dfrac{bc}{\left(a+b\right)\left(a+c\right)}+\dfrac{ac}{\left(a+b\right)\left(b+c\right)}+\dfrac{ab}{\left(a+c\right)\left(b+c\right)}\right)\)
\(=\dfrac{2abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)
2. Do ABC cân tại C \(\Rightarrow AC=BC=a\)
\(\dfrac{BC}{AB}=k\Rightarrow AB=\dfrac{BC}{k}=\dfrac{a}{k}\)
Do đó:
\(\dfrac{S_{MNP}}{S_{ABC}}=\dfrac{2abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=\dfrac{2.a.a.\dfrac{a}{k}}{2a.\left(a+\dfrac{a}{k}\right)\left(a+\dfrac{a}{k}\right)}=\dfrac{k}{\left(k+1\right)^2}\)

\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{9}{a+b+c}\ge4\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{a+c}\right)\)
\(\Leftrightarrow\dfrac{a+b+c}{a}+\dfrac{a+b+c}{b}+\dfrac{a+b+c}{c}+9\) \(\ge4\left(a+b+c\right)\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{a+c}\right)\)
\(\Leftrightarrow\dfrac{b+c}{a}+\dfrac{a+c}{b}+\dfrac{a+b}{c}+12\ge4\left(3+\dfrac{c}{a+b}+\dfrac{a}{b+c}+\dfrac{b}{a+c}\right)\)
\(\Leftrightarrow\dfrac{b+c}{a}+\dfrac{a+c}{b}+\dfrac{a+b}{c}\ge4\left(\dfrac{c}{a+b}+\dfrac{a}{b+c}+\dfrac{b}{a+c}\right)\).
Áp dụng bất đẳng thức \(\dfrac{1}{a+b}\le\dfrac{1}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\) ta có:
\(\dfrac{c}{a+b}+\dfrac{a}{b+c}+\dfrac{b}{a+c}\le\dfrac{1}{4}\left(\dfrac{c}{a}+\dfrac{c}{b}+\dfrac{a}{b}+\dfrac{a}{c}+\dfrac{b}{a}+\dfrac{b}{c}\right)\) \(=\dfrac{1}{4}\left(\dfrac{b+c}{a}+\dfrac{a+c}{b}+\dfrac{a+b}{c}\right)\).
Suy ra \(4\left(\dfrac{c}{a+b}+\dfrac{a}{b+c}+\dfrac{b}{a+c}\right)\le\dfrac{b+c}{a}+\dfrac{a+c}{b}+\dfrac{a+b}{c}\) 9 (đpcm).

Vì BC có độ dài lớn nhất nên đề bài tương đương với: \(\sqrt[3]{BD^2}+\sqrt[3]{EC^2}=\sqrt[3]{BC^2}\)(Định lí Pythagoras đảo)
Lập phương 2 vế: \(BD^2+EC^2+3\sqrt[3]{\left(BD.EC\right)^2}\left(\sqrt[3]{BD^2}+\sqrt[3]{EC^2}\right)=BC^2\)
Ôn lại các hệ thức lượng cho tam giác vuông vì sắp tới mình sẽ dùng 1 chuỗi hệ thức đấy:
+Tam giác AHD vuông tại H, đường cao DH: \(AH^2=AD.AB,BH^2=BD.BA\)
+Tam giác AHC vuông tại H, đường cao EH: \(AH^2=AC.AE,CH^2=CA.CE\)
+Tam giác ABC vuông tại A, đường cao AH: \(AH^2=HB.HC,AH.BC=AB.AC,BC^2=AB^2+AC^2\)
$ ADHE là hình chữ nhật nên AD=HE
$ Tam giác AHE vuông tại H nên \(AH^2=AE^2+HE^2\)
Ok, giờ triển thoi: \(BD^2+EC^2+3\sqrt[3]{\left(BD.EC\right)^2}\left(\sqrt[3]{BD^2}+\sqrt[3]{EC^2}\right)=BC^2\)
\(\Leftrightarrow\left(AB-AD\right)^2+\left(AC-AE\right)^2+3\sqrt[3]{\left(BD.CE\right)^2}.\sqrt[3]{BC^2}=BC^2\)
\(\Leftrightarrow\left(AB^2+AC^2\right)+\left(AD^2+AE^2\right)-2\left(AB.AD+AC.AE\right)+3\sqrt[3]{\left(BD.CE.BC\right)^2}=BC^2\)
\(\Leftrightarrow BC^2+\left(AE^2+HE^2\right)-2\left(AH^2+AH^2\right)+3\sqrt[3]{\left(BD.CE.BC\right)^2}=BC^2\)
\(\Leftrightarrow AH^2-4AH^2-3\sqrt[3]{\left(BD.CE.BC\right)^2}=0\)
\(\Leftrightarrow3\sqrt[3]{\left(BD.CE.BC\right)^2}=3AH^2\)
\(\Leftrightarrow BD.CE.BC=AH^3\)
\(\Leftrightarrow BD.CE.BC.AH=AH^4\)
\(\Leftrightarrow\left(BD.BA\right)\left(CE.CA\right)=AH^4\)
\(\Leftrightarrow BH^2.CH^2=AH^4\Leftrightarrow BH.CH=AH^2\)---> Luôn đúng
Vậy giả thiết đúng.
(Bài dài giải mệt vler !!)

Áp dụng BĐT:1/a+1/b>=4/a+b
Ta có:
1/(p-a)+1/(p+b)>=4/(2p-a-b)=4/c
Các phần sau tương tự!
=>2VT>=4(1/a+1/b+1/c)
=>VT>=2(1/a+1/b+1/c)
b)
Dấu "=" xảy ra p-a=p-b=p-c => a=b=c
=>tg đều

Gọi độ dài 3 cạnh DABC lần lượt là a,b,c. Đường cao hạ từ các đỉnh A,B,C là x,y,z. Bán kính đường tròn nội tiếp tam giác ABC = 1. Khi đó ta có
SABC=1/2ax=1/2by=1/2cz=1/2(a+b+c)r
=> ax = by = cz = a+b+c [*]
ta có:
ax = by = cz => a: (1/ x)= b:(1/ y)=c:(1/z)
=> (a+b+c): (1/x+1/y+1/z) = a+b+c
=> (1/x+1/y+1/z) = 1
Giả sử: 0 ≤ x ≤ y ≤ z =>1/x ≥1/y ≥ 1/z => 3/x ≤ 1 => x ≤ 3
Thử từng trường hợp:
*x=1. => Loại
*x=2 =>1/y+1 / z= ½. Mà x,y ϵ Z
=>y,z ϵ {(4,4);(3;6)}
y = z = 4 => 2a = 4b = 4c Áp dụng BDT tam giác vào tam giác ABH thấy ko thỏa mãn=>loại
y=3;z=4⇒2a=3b=4c (loại)
*x=3
x = y = z = 3 => a=b=c=> tam giácABC:đều (đpcm).

Ta có \(a,b,c\)và \(a',b',c'\)là độ dài các cạnh tương ứng của 2 tam giác đồng dạng
Đương nhiên \(\frac{a}{a'}=\frac{b}{b'}=\frac{c}{c'}=k\left(k>0\right)\). Khi đó:
\(\sqrt{aa'}+\sqrt{bb'}+\sqrt{cc'}=\sqrt{k}\left(a'+b'+c'\right)\)(1)
\(\sqrt{\left(a+b+c\right)\left(a'+b'+c'\right)}=\sqrt{k\left(a'+b'+c'\right)^2}=\sqrt{k}\left(a'+b'+c'\right)\)(2)
Từ (1) và (2) suy ra ĐPCM.
Áp dụng BĐT AM-GM ta có:
\(\dfrac{abc}{a^2+bc}\le\dfrac{abc}{2a\sqrt{bc}}=\dfrac{\sqrt{bc}}{2}\le\dfrac{b+c}{4}\)
Tương tự cho 2 BĐT còn lại rồi cộng theo vế:
\(abc.VT\le\dfrac{2\left(a+b+c\right)}{4}=1\Leftrightarrow VT\le\dfrac{1}{abc}=VP\)
Dấu "="\(\Leftrightarrow a=b=c=\dfrac{2}{3}\)