Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

giải thích cặn kẽ như sau:
do xe máy và xe đạp di chuyển ngược nhau và gặp nhau tại một điểm nên ta có:
t1=t2(t1 là của xe máy,t2 là của xe đạp)
\(\Leftrightarrow\frac{S_1}{v_1}=\frac{S_2}{v_2}\)
\(\Leftrightarrow\frac{S_1}{30}=\frac{S_2}{10}\)
mà quãng đường xe máy cộng quãng đường xe đạp bằng quãng đường AB(S1+S2=S=60)(cái này vẽ sơ đồ là biết)
\(\Rightarrow S_2=60-S_1\)
thế vào phương trình trên ta có:
\(\frac{S_1}{30}=\frac{60-S_1}{10}\)
giải phương trình ta được S1=45km,S2=15km
từ đó ta có t1=1.5 giờ và điểm gặp cách A 45km
Gọi t là thời gian 2 xe gặp nhau:
Vì 2 xe đi ngược chiều nên
t= \(\frac{s}{v_1+v_2}=\frac{60}{30+10}=\frac{3}{2}=1,5\left(h\right)=1h30'\)
Vị trí gặp nhau đó cách A:
L=v1.t= 30.1,5=45(km)

gọi thời gian đi tới khi gặp xe một của xe ba là t3
thời gian đi tới khi gặp xe hai của xe ba là t3'
30'=0,5h
ta có:
lúc xe ba gặp xe một thì:
\(S_1=S_3\)
\(\Leftrightarrow v_1t_1=v_3t_3\)
do xe ba đi sau xe một 30' nên:
\(v_1\left(t_3+0,5\right)=v_3t_3\)
\(\Leftrightarrow10\left(t_3+0,5\right)=v_3t_3\)
\(\Leftrightarrow10t_3+5=v_3t_3\)
\(\Leftrightarrow v_3t_3-10t_3=5\)
\(\Rightarrow t_3=\frac{5}{v_3-10}\left(1\right)\)
ta lại có:
lúc xe ba gặp xe hai thì:
\(S_3=S_2\)
\(\Leftrightarrow v_3t_3'=v_2t_2\)
do xe hai đi trước xe ba 30' nên:
\(v_3t_3'=v_2\left(t_3'+0,5\right)\)
\(\Leftrightarrow v_3t_3'=12\left(t_3'+0,5\right)\)
tương tự ta có:
\(t_3'=\frac{6}{v_3-12}\left(2\right)\)
do thời gian gặp cả hai lần cách nhau một giờ nên:
t3'-t3=1
\(\Leftrightarrow\frac{6}{v_3-12}-\frac{5}{v_3-10}=1\)
\(\Leftrightarrow\frac{6\left(v_3-10\right)-5\left(v_3-12\right)}{\left(v_3-12\right)\left(v_3-10\right)}=1\)
\(\Leftrightarrow6v_3-60-5v_3+60=\left(v_3-12\right)\left(v_3-10\right)\)
\(\Leftrightarrow v_3=v_3^2-10v_3-12v_3+120\)
\(\Leftrightarrow v_3^2-23v_3+120=0\)
giải phương trình bậc hai ở trên ta được:
v3=15km/h
v3=8km/h(loại)
bn xem lại chỗ: k/c giữa 2 lần gặp của ng3 voi 2 ng đi trc là 1h?
(k thể như z dc vì v1 khác v2 nên k thể găp 2 ng cùng lúc 1h)

Khi người thứ ba gặp người thứ nhất:
\(x_1=x_3\)\(\Rightarrow10t=v_3\left(t_1-\dfrac{2}{3}\right)\)\(\Rightarrow t_1=\dfrac{\dfrac{2}{3}v_3}{v_3-10}\)
Khi người 3 cách đều người 1 và người 2:
\(x_3=\dfrac{x_1+x_2}{2}=\dfrac{10t_2+20t_2-10}{2}=15t_2-5\left(km\right)\)
\(\Rightarrow v_3\cdot\left(t_2-\dfrac{2}{3}\right)=15t_2-5\)
Ta có: \(t_2-t_1=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{\dfrac{2}{3}v_3-5}{v_3-15}-\dfrac{\dfrac{2}{3}v_3}{v_3-10}=\dfrac{2}{3}\)
\(\Rightarrow\left[{}\begin{matrix}v_3=18,43\\v_3=4,07\end{matrix}\right.\)

Câu 1)
Người thứ nhất đi đc trong 30p
\(s_1=v_1t=10,0.5=5\left(km\right)\)
Ng thứ 2 đi đc trong 30p
\(s_2=v_2t=12.0,5=6km\)
Gọi v3 là vận tốc của ng thứ 3, t1 t2 là khoảng tgian khi ng thứ 3 xuất phát và gặp ng thứ nhất và ng thứ 2
Khi ng thứ 3 gặp ng thứ nhất
\(v_3t_1=5+10t_1\\ \Rightarrow t_1=\dfrac{5}{v_3-10}\left(1\right)\)
Khi gặp ng thứ 2
\(v_3t_2=6+12t_2\\ \Rightarrow t_2=\dfrac{6}{v_3-12}\left(2\right)\)
Theo đề bài + từ (1) và (2)
\(\Rightarrow v_3=15km/h\)

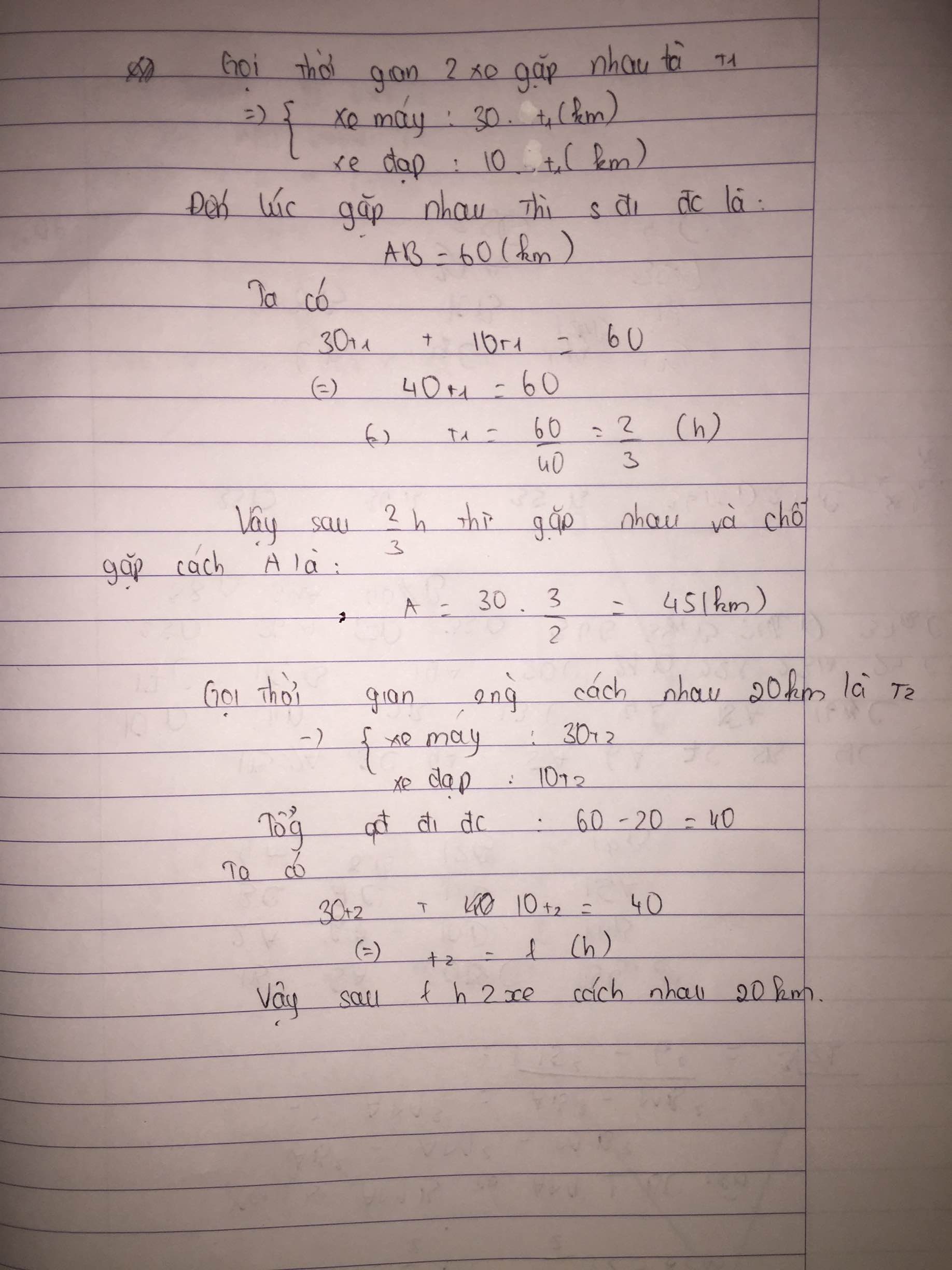
chọn mốc thời gian là thời điểm xe 1 xuất phát
phương trình chuyển động của 3 người là:
\(S_1\)=\(v_1.t\)=20t
\(S_2\)=\(v_2.\left(t-1\right)\)=10t-10
\(S_3\)=\(v_3.\left(t-1,5\right)\)=30t-45
thời gian để người thứ 3 cách đều người thứ 1 và thứ 2 là:
\(S_3=\frac{S_1+S_2}{2}\)
<=> 30t-45=\(\frac{20t+10t-10}{2}\)
<=> 30t-45=\(\frac{30t-10}{2}\)
<=>2.(30t-45)=30t-10
<=> 60t-90=30t-10
<=> 60t-30t=90-10
<=> 30t =80
<=> t =\(\frac{8}{3}\) (h)
vậy thời điểm người thứ 3 cách đều người thứ 1 và thứ 2 là:
6+\(\frac{8}{3}\)=\(\frac{26}{3}\) hay 8h40 phút
K bt đúng hay sai nx nếu sai mong bn thông cảm
