Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC vuông tại A và ΔDEF vuông tại D có
AB/DE=AC/DF
Do đó: ΔABC\(\sim\)ΔDEF
b: \(\dfrac{C_{ABC}}{C_{DEF}}=\dfrac{AB}{DE}=\dfrac{2}{3}\)

Hướng dẫn cách hack VIP OLM Vĩnh Viễn siêu dễ chỉ 10 phút là xong: youtube.com/watch?v=zYcnHqUcGZE&t

Ta có : \(\Delta ABC\sim\Delta A'B'C'\)
\(\Rightarrow\dfrac{P_{ABC}}{P_{A'B'C'}}=\dfrac{AB}{A'B'}=\dfrac{2}{7}\)
\(\Rightarrow\dfrac{P_{ABC}}{2}=\dfrac{P_{A'B'C'}}{7}=\dfrac{P_{ABC}+P_{A'B'C'}}{2+7}=\dfrac{180}{9}=20\)
( tính chất dãy tỉ số bằng nhau )
\(\Rightarrow P_{ABC}=2.20=40\left(cm\right)\)
\(\Rightarrow P_{A'B'C'}=20.7=140\left(cm\right)\)

6.)
Khi 2 tam giác đồng dạng với nhau thì cạnh nhỏ nhất của tam giác này sẽ tương ứng với cạnh nhỏ nhất của tam giác kia.
Theo đề:\(A'B'\)=4,5
Ta có:\(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)
\(\Rightarrow\)\(\frac{4,5}{3}=\frac{B'C'}{5}=\frac{C'A'}{7}\)
\(\Rightarrow\)\(B'C'=7,5cm,C'A'=10,5cm\)

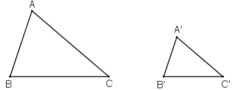
a) Gọi chu vi tam giác A’B’C’ là P’ và chu vi tam giác ABC là P.
ΔA'B'C' 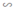 ΔABC theo tỉ số đồng dạng k = 3/5
ΔABC theo tỉ số đồng dạng k = 3/5
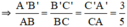
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
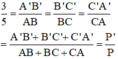
Vậy tỉ số chu vi tam giác A’B’C’ và tam giác ABC là 3/5
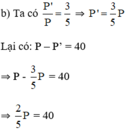
⇒ P = 100 ⇒ P’ = 60.
Vậy chu vi tam giác ABC bằng 100dm và chu vi tam giác A’B’C’ là 60dm.

a: Ta có: ΔA'B'C'∼ΔABC
nên A'B'/AB=B'C'/BC=A'C'/AC
=>A'B'/6=B'C'/12=A'C'/8=3/2
=>A'B'=9cm; B'C'=18cm; A'C'=12cm
b: Ta có: ΔA'B'C'∼ΔABC
nên \(\dfrac{C_{A'B'C'}}{C_{ABC}}=\dfrac{3}{2}\)
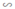 ΔABC theo tỉ số đồng dạng k = 3/5.
ΔABC theo tỉ số đồng dạng k = 3/5.

1/ A B C D E F
Ta có: \(\frac{12}{16}=\frac{9}{12}=\frac{15}{20}=\frac{3}{4}\Leftrightarrow\frac{AB}{DE}=\frac{BC}{EF}=\frac{CA}{FD}\)
suy ra Tam giác ABC đồng dạng với tam giác DEF
Nên \(\left\{{}\begin{matrix}\widehat{ABC}=\widehat{DEF}\\\widehat{ACB}=\widehat{DFE}\\\widehat{BAC}=\widehat{EDF}\end{matrix}\right.\) (2 góc tương ứng)