Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBEC và ΔCDB có
BE=CD
\(\widehat{EBC}=\widehat{DCB}\)
BC chung
Do đó: ΔBEC=ΔCDB
Suy ra: CE=DB
b: Xét ΔGBC có \(\widehat{GCB}=\widehat{GBC}\)
nên ΔGBC cân tại G
=>GB=GC
Ta có: GB+GD=BD
GE+GC=CE
mà BD=CE
và GB=GC
nên GD=GE
hay ΔGDE cân tại G
c: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
Ta có: GB=GC
nên G nằm trên đường trung trực của BC(2)
Ta có: MB=MC
nên M nằm trên đường trung trực của BC(3)
Từ (1), (2) và (3) suy ra A,G,M thẳng hàng

a: ΔABC cân tại A
=>AB=AC
mà AB=8
nên AC=8
Xét ΔDAB có
E,M lần lượt là trung điểm của DA,DB
=>EM là đường trung bình của ΔDAB
=>EM//AB và \(EM=\dfrac{AB}{2}=4\)
Xét ΔDBC có
M,F lần lượt là trung điểm của DB,DC
=>MF là đường trung bình của ΔDBC
=>MF//BC và \(MF=\dfrac{BC}{2}=\dfrac{9}{2}=4,5\)
AD+DC=AC
=>2*ED+2*DF=AC
=>AC=2EF
=>\(EF=\dfrac{AC}{2}=4\)
Chu vi tam giác MEF là:
\(C_{MEF}=EF+EM+MF=4+4+4,5=12,5\)
b: \(\dfrac{AB+AD}{2}=\dfrac{AC+AD}{2}=\dfrac{AD+DC+AD}{2}\)
\(=\dfrac{2AD+2DF}{2}=AD+DF=AF\)

A B C D E i H
A) Ta có tam giác ABC cân
=> AB = AC
Mà AD + DB = AB
AE + EC = AC
=> DB = EC ( AD = AE gt)
b) đề phải là BE và CD cắt nhau tại I
Ta có AD = AE
=> Tam giác ADE cân tại A
=> Góc ADE = Góc AED
=> Góc EDB = Góc DEC ( Cùng cộng nhau bằng 180 độ )
Xét Tam giác DEB và tám giác EDC có
BD = EC (cmt)
Góc EDB = Góc DEC (cmt)
DE là cạnh chung
=> Tam giác DEB và tam giác EDC (c-g-c)
=> Góc DBE = Góc ECD
=> Góc IBC = Góc ICB ( cùng cộng góc DBE và Góc ECD bằng hai góc ABC và Góc ACB)
=> Tam giác IBC cân
c) Ta có tam giác ADE cân \(\Leftrightarrow\widehat{ADE}=\frac{180^o-\widehat{A}}{2}\left(1\right)\)
Và tam giác ABC cân \(\Leftrightarrow\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\left(2\right)\)
Từ (1) và (2)\(\Leftrightarrow\widehat{ADE}=\widehat{ABC}\)
Hai góc này ở vị trí đồng vị bằng nhau
=> DE // BC (đpcm)
d) Ta có điểm I cách đều cạnh AB và AC
=> AI là tia phân giác của tam giác ABC
trong tam giác cân tia phân giác cũng là đường cao
=> AI vuông góc với BC
E) chứng minh HI là tia phân giác của tam giác BHC
thì ba điểm thẳng hàng

a) Xét ΔAMB và ΔAMC có
AB=AC(gt)
MB=MC(M là trung điểm của BC)
AM chung
Do đó: ΔAMB=ΔAMC(c-c-c)
b) Sửa đề: AM=MD
Xét ΔAMC và ΔDMB có
AM=DM(gt)
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB(M là trung điểm của BC)
Do đó: ΔAMC=ΔDMB(c-g-c)
⇒AC=DB(Hai cạnh tương ứng)
c) Ta có: ΔAMC=ΔDMB(cmt)
nên \(\widehat{ACM}=\widehat{DBM}\)(hai góc tương ứng)
mà \(\widehat{ACM}\) và \(\widehat{DBM}\) là hai góc ở vị trí so le trong
nên AC//BD(Dấu hiệu nhận biết hai đường thẳng song song)


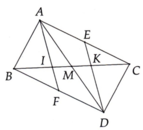
Bài 1:
a: Xét ΔABD có E,I lần lượt là trung điểm của BA,BD
=>EI là đường trung bình của ΔABD
=>EI//AD và EI=AD/2
EI//AD
D\(\in\)AC
Do đó: EI//AC
Xét ΔBDC có
I,M lần lượt là trung điểm của BD,BC
=>IM là đường trung bình của ΔBDC
=>IM//DC và IM=DC/2
IM//DC
D\(\in\)AC
Do đó: IM//AC
IM//AC
EI//AC
IM,EI có điểm chung là I
Do đó: E,I,M thẳng hàng
Xét ΔBEC có
M,K lần lượt là trung điểm của CB,CE
=>MK là đường trung bình của ΔBEC
=>MK//EB và MK=EB/2
MK//EB
E\(\in\)AB
Do đó: MK//AB
Xét ΔACE có
D,K lần lượt là trung điểm của CA,CE
=>DK là đường trung bình của ΔAEC
=>DK//AE và DK=AE/2
DK//AE
E\(\in\)AB
Do đó: DK//AB
DK//AB
MK//AB
DK,MK có điểm chung là K
Do đó: D,M,K thẳng hàng
b: MI=DC/2
EI=AD/2
mà AD=DC
nên MI=EI
=>I là trung điểm của ME
MK=BE/2
DK=AE/2
mà BE=AE
nên MK=DK
=>K là trung điểm của DM
Xét ΔMED có
I,K lần lượt là trung điểm của ME,MD
=>IK là đường trung bình
=>IK//ED và IK=ED/2
c: Xét ΔABC có
E,D lần lượt là trung điểm của AB,AC
=>ED là đường trung bình của ΔABC
=>\(ED=\dfrac{BC}{2}\)
\(IK=\dfrac{ED}{2}=\dfrac{BC}{2}:2=\dfrac{BC}{4}=\dfrac{4}{4}=\dfrac{4}{4}=1\left(cm\right)\)
Cậu giúp dc mik câu 2 k ạ chứ mình ngồi mãi mà làm k ra hichic