Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số sách của 2 lớp 7A & 7B lần lượt là a và b.
Theo t/c dãy tỉ số = nhau ta có:
\(\frac{a}{5}=\frac{b}{7}=\frac{a+b}{5+7}=\frac{120}{12}=10\)
=> a/5=10 => a=10.5=50 (cuốn)
=> b/7=10 => b=10.7=70 (cuốn)
Vậy ...

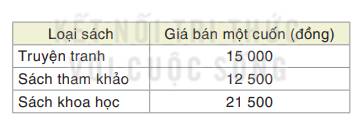
`a,` Đa thức biểu thị số tiền sách khoa học là:
`21500*x` (đồng)
Đa thức biểu thị số tiền sách truyện tranh là:
`15000*(x+5)` (đồng)
Đa thức biểu thị số tiền sách tham khảo là:
`12500(x+8)`(đồng)
`b,`
Đa thức biểu thị số tiền Nam phải trả là:
`21500*x+12500(x+8)+15000(x+5)`
`= 21500*x+12500x+100000+15000x+75000`
`= (21500x+12500x+15000x)+(100000+75000)`
`= 49000x+175000`
Vậy, đa thức biểu thị số tiền Nam phải trả là `49000x+175000 (`đồng `).`
a: Số tiền phải trả cho truyện tranh là 15000(x+5)=15000x+75000(đồng)
Số tiền phải trả cho sách tham khảo là:
12500(x+8)=12500x+100000(đồng)
Số tiền phải trả cho sách khoa học là:
21500x(đồng)
b: Tổg số tiền là:
15000x+75000+12500x+100000+21500x=49000x+175000(đồng)

Số sách giáo khoa:
120 . 2/3 = 80 (quyển)
Số sách tham khảo:
120 - 80 = 40 (quyển)

a) Đa thức biểu thị số tiền Nam phải trả cho truyện tranh là: A = (x +5). 15 000 = 15 000x + 75 000 ( đồng)
Đa thức biểu thị số tiền Nam phải trả cho sách tham khảo là: B = (x + 8) . 12 500 = 12 500x + 100 000 ( đồng)
Đa thức biểu thị số tiền Nam phải trả cho sách khoa học là: C = x . 21 500 (đồng)
b) Đa thức biểu thị tổng số tiền Nam phải trả để mua số sách đó là:
P = A + B + C = = 15 000x + 75 000 + 12 500x + 100 000 + x . 21 500
= (15 000 + 12 500 + 21 500)x + (75 000 + 100 000)
= 49 000x + 175 000 ( đồng)

Toán này lớp 4 là giải được :
Các số có 2 chữ số thì trung bình cộng của chúng là 2 chữ số
Các số có 1 chữ số phải kết hợp với số có 3 chữ số ra TBC 2 chữ số
Có 9 số có 1 chữ số nên phải kết hợp với 9 số ó hai chữ số : từ 100 đến 108 (108 nha KHÔNG PHẢI 109 )

Gọi số cuốn sách tham khảo môn Toán lớp 6, lớp 7 và lớp 8 mà thư viện đó mua lần lượt là x, y, z (x, y, z \( \in \)\(\mathbb{N}\))
Vì tổng cộng là 121 cuốn nên ta có \(x + y + z = 121\)
Vì số tiền dùng để mua mỗi loại sách đó là như nhau nên số cuốn sách và giá tiền một cuốn sách tương ứng là 2 đại lượng tỉ lệ nghịch.
Theo tính chất hai đại lượng tỉ lệ nghịch, ta có:
\(40.x=45.y=50.z \Rightarrow \dfrac{x}{{\dfrac{1}{{40}}}} = \dfrac{y}{{\dfrac{1}{{45}}}} = \dfrac{z}{{\dfrac{1}{{50}}}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{{\dfrac{1}{{40}}}} = \dfrac{y}{{\dfrac{1}{{45}}}} = \dfrac{z}{{\dfrac{1}{{50}}}}= \dfrac{{x + y + z}}{{\dfrac{1}{{40}} + \dfrac{1}{{45}} + \dfrac{1}{{50}}}} = \dfrac{{121}}{{\dfrac{{121}}{{1800}}}} = 121.\dfrac{{1800}}{{121}} = 1800\\ \Rightarrow x = 1800.\dfrac{1}{{40}} = 45\\y = 1800.\dfrac{1}{{45}} = 40\\z = 1800.\dfrac{1}{{50}} = 36\)
Vậy số sách tham khảo môn Toán lớp 6, lớp 7 và lớp 8 mà thư viện đó mua lần lượt là 45 quyển, 40 quyển và 36 quyển.

Số sách ở ngăn thứ nhất là: 180.1/3=60 (cuốn)
Số sách còn lại là: 180-60= 120 (cuốn)
Gọi số sách ở ngăn thứ hai là x, số sách ở ngăn thứ hai là y.
Theo bài ra ta có: x=1/2y => 2x=y (1)
Lại có: x+y= 120 (2)
Thay (1) vào (2) ta được: x+2x=120
<=> 3x=120
<=> x=120:3=40 (cuốn)
hay ngăn thứ hai có 40 cuốn sách.
Số sách ở ngăn thứ ba là: 120-40=80 (cuốn)
Vậy ngăn thứ nhất có 60 cuốn sách
ngăn thứ hai có 40 cuốn sách
ngăn thứ ba có 80 cuốn sách
Gọi số sách ở 3 ngăn là a, b, c ( \(a,b,c\inℕ^∗;a,b,c< 180\))
Theo bài ra, ta có : \(a=\frac{a+b+c}{3}\)và \(\frac{b}{c}=\frac{1}{2}\)
Từ \(a=\frac{a+b+c}{3}\)\(\Rightarrow a=\frac{180}{3}=60\)
Từ \(\frac{b}{c}=\frac{1}{2}\)\(\Rightarrow\frac{b}{1}=\frac{c}{2}=\frac{b+c}{1+2}=\frac{180-a}{3}=\frac{180-60}{3}=\frac{120}{3}=40\)
\(\Rightarrow b=40.1=40\); \(c=40.2=80\)
Vậy số sách ở 3 ngăn lần lượt là: 60, 40, 80 quyển sách