K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
23 tháng 10 2016
Không nên đăng những thứ này nhưng chúng ta có thể nói chuyện với nhau mà
AH
Akai Haruma
Giáo viên
22 tháng 8 2023
1.
$A=2+2^2+2^3+2^4+...+2^{10}$
$=(2+2^2+2^3+2^4)+(2^5+2^6+2^7+2^8)+2^9+2^{10}$
$=2(1+2+2^2+2^3)+2^5(1+2+2^2+2^3)+2^9(1+2)$
$=15(2+2^5)+3.2^9$
Ta thấy $15(2+2^5)\vdots 5$ còn $3.2^9\not\vdots 5$
$\Rightarrow A\not\vdots 5$
AH
Akai Haruma
Giáo viên
22 tháng 8 2023
Bài 2:
$B=2+2^2+2^3+2^4+...+2^{99}+2^{100}$
$=(2+2^2)+(2^3+2^4)+(2^5+2^6)+...+(2^{99}+2^{100})$
$=2(1+2)+2^3(1+2)+2^5(1+2)+...+2^{99}(1+2)$
$=(1+2)(2+2^3+2^5+...+2^{99})$
$=3(2+2^3+2^5+...+2^{99})\vdots 3$
BD
22 tháng 8 2023
3.
\(C=5+5^2+...+5^6\\ C=5\left(1+5\right)+5^3\left(1+5\right)+5^5\left(1+5\right)\\ C=5\cdot6+5^3\cdot6+5^5\cdot6\\ C=6\left(5+5^3+5^5\right)\\ =>C⋮6\)
\(4.D=3+3^2+...+3^6\\D=3\left(1+3\right)+3^3\left(1+3\right)+3^5\left(1+3\right)\\ D=3\cdot4+3^3\cdot4+3^5\cdot5\\ C=4\left(3+3^3+3^5\right)\\ =>D⋮4\\ 5.E=4+4^2+...+4^6\\ E=4\left(1+4\right)+4^3\left(1+4\right)+4^5\left(1+4\right)\\ E=4\cdot5+4^3\cdot5+4^5\cdot5\\ E=5\left(4+4^3+4^5\right)=>E⋮5 \)
HT
2
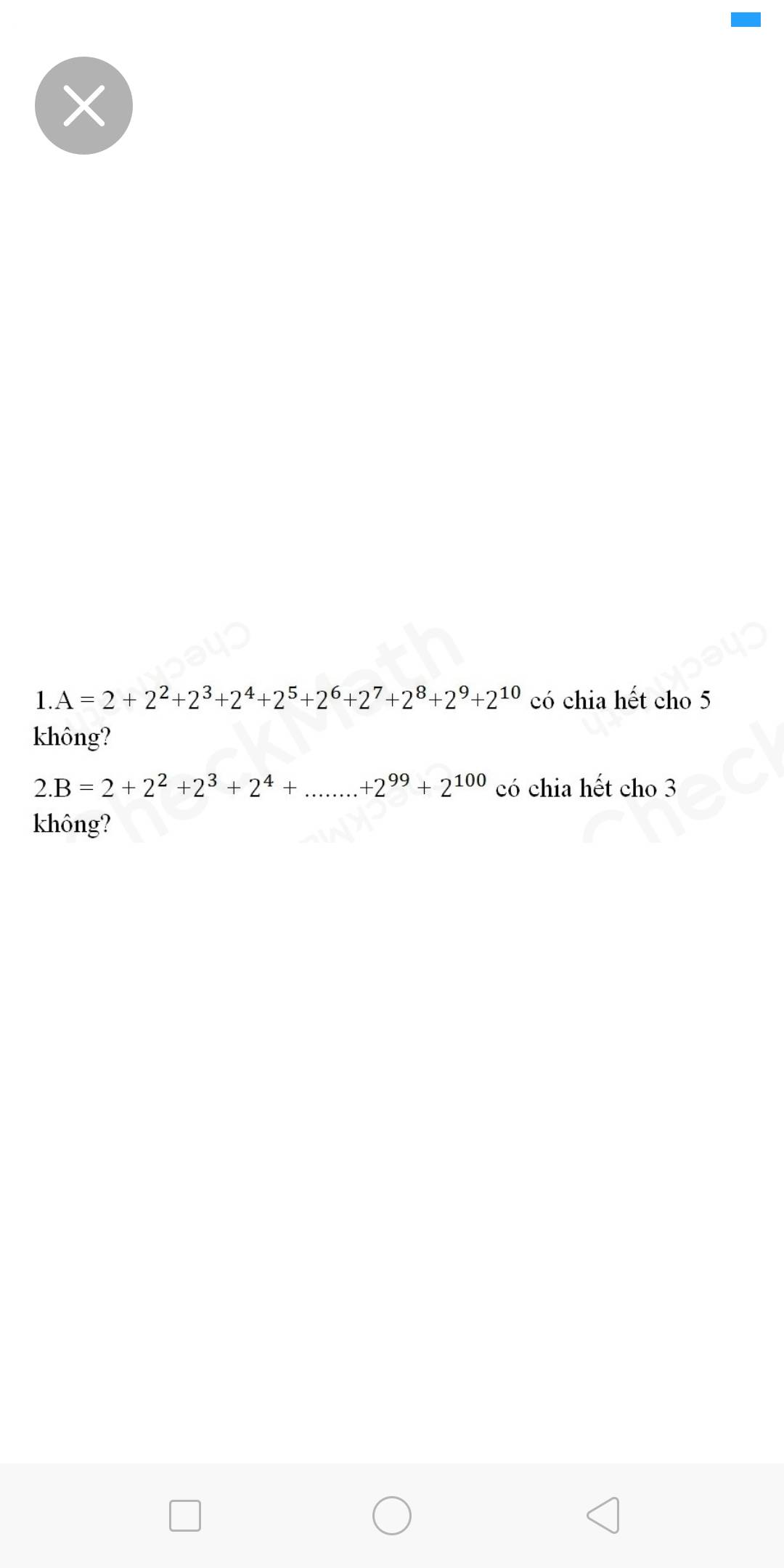
mk đk hơm